Axes de symétrie
Axes de symétrie
AXES DE SYMETRIE
Définition
Une droite est un axe de symétrie d’une figure lorsque cette figure est son propre symétrique par rapport à cet axe.
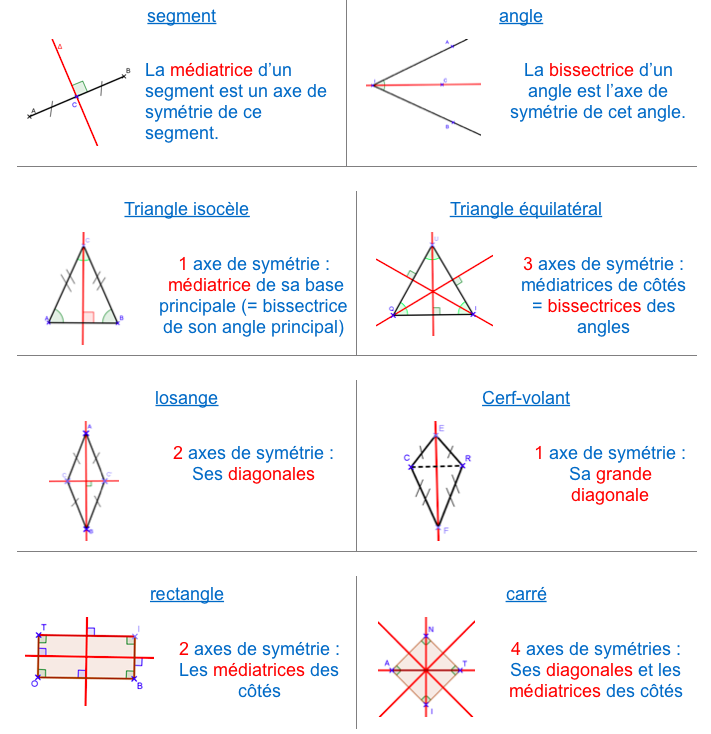
Les axes de symétrie des figures usuelles
Parallélogrammes
Parallélogrammes
Définition :
Un parallélogramme est un quadrilatère dont les côtés opposés sont parallèles.
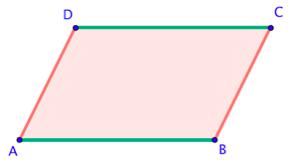
Voici un parallélogramme ABCD :
On a :
- $(AB)$//$(DC)$
- $(AD)$//$(BC)$
Commentaires :
Si un quadrilatère est un parallélogramme, alors ses côtés opposés sont (deux à deux) parallèles.
Si les côtés opposés d’un quadrilatère sont (2 à 2) parallèles, alors il s’agit d’un parallélogramme.
Propriétés
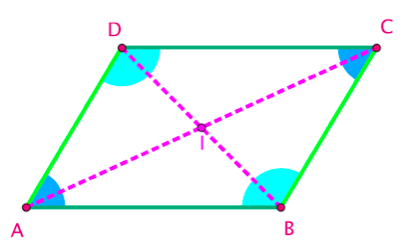
Si un quadrilatère est un parallélogramme, alors :
- Ses diagonales (en rose) se coupent en leurs milieux (noté I sur la figure)
- Ses côtés opposés (en vert clair ou vert foncé) sont de même longueur.
- Ses angles opposés sont de même mesure
- De plus, la somme de deux angles consécutifs (qui se suivent) est égale à 180°.
Le plus des bons profs
Les losanges, rectangles ou carrés sont tous des parallélogrammes particuliers (car ils ont bien des cotés opposés parallèles)
Le cercle
Le cercle
Définition
Un cercle est formé de tous les points situés à la même distance d’un point appelé « centre ».
Cette distance commune est appelée « rayon ».
Si $\mathcal{C}$ est le cercle de centre $O$ et de rayon $r$, l’écriture « $M \in \mathcal{C}$ » signifie que la distance $OM$ est égale à $r$
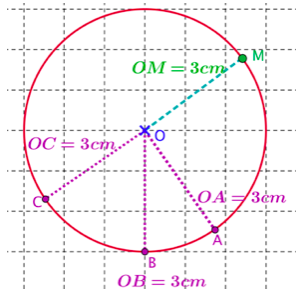
Exemple :
si $\mathcal{C}$ est le cercle de centre $O$ et de rayon $3$cm, $M \in \mathcal{C}$ signifie que $OM=3$cm
Vocabulaire
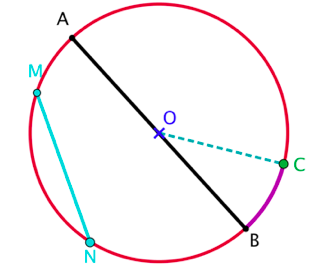
Soit $\mathcal{C}$ le cercle de centre $O$ et de rayon $r$, où $r$ est un nombre positif donné.
Si $C$ est un point du cercle $\mathcal{C}$ on dit que le segment $[OC]$ est un rayon du cercle.
Si $M$ et $N$ sont deux points du cercle $\mathcal{C}$ on dit que le segment $[MN]$ est une corde du cercle.
Une corde passant par le centre du cercle est appelée diamètre du cercle $\mathcal{C}$. Par exemple, le segment $[AB]$ est un diamètre du cercle.
La portion du cercle comprise entre les points $B$ et $C$ est un arc de cercle.
Le petit plus des bons profs
Deux formules supplémentaires sur le cercle à retenir:
Etant donné un cercle de rayon $R$
- Le périmètre du cercle est égal à : $P= 2\pi R$
- L’ aire du disque est égale à : $A=\pi R^2$
La médiatrice d'un segment
Médiatrice d’un segment
Définition
La médiatrice d’un segment est la droite perpendiculaire à ce segment en son milieu.
G est le milieu du segment [AB] et $d \perp (AB)$ donc d est la médiatrice du segment [AB].
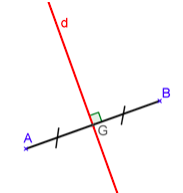
Propriété de la médiatrice :
La médiatrice d’un segment est l’ensemble des points du plan équidistants des extrémités de ce segment.
Remarque : équidistant signifie « à égale distance ».
On a en fait deux propriétés :
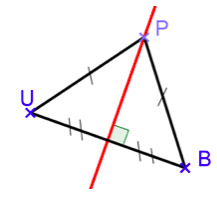
Si un point P appartient à la médiatrice du segment [UB] alors PU=PB (c’est-à-dire P est équidistant des extrémités du segment [UB]).
Si un point P est équidistant des extrémités d’un segment [UB] (c’est-à-dire si PU=PB) alors P appartient à la médiatrice de [UB].
Commentaires
-Grâce à ces propriétés nous avons une construction au compas.
-Cela signifie aussi que tous les points qui n’appartiennent pas à la médiatrice d’un segment ne sont pas équidistants des extrémités de ce segment. Ils sont donc plus proches de l’une des deux extrémités que de l’autre.
Le petit plus des Bons Profs
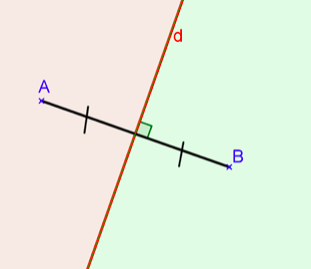
On a ainsi un partage du plan en trois parties : les points de la médiatrice du segment, les points du demi-plan rose et ceux du demi-plan vert ci-dessous
En rose, un demi-plan : les points plus proches du point A ; En vert, un demi-plan : les points plus proches du point B
