Fonctions convexes et concaves
Fonctions convexes et concaves
Définition
Soit $f$ une fonction dérivable sur un intervalle $I$,
$f$ est convexe sur $I$ lorsque sa courbe est entièrement située au dessus de chacune de ses tangentes.
Il s’agit donc d’une notion locale, définie sur un intervalle.
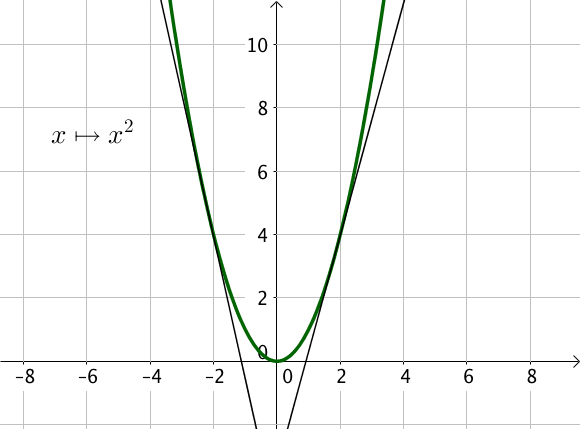
Par exemple, la fonction $y = x^2$ est convexe sur $\mathbb{R}$.
Pour démonter la convexité d’une fonction, on utilisera d’autres propriétés plus efficaces que cette notion graphique.
$f$ est concave sur $I$ lorsque sa courbe est entièrement située en dessous de chacune de ses tangentes.
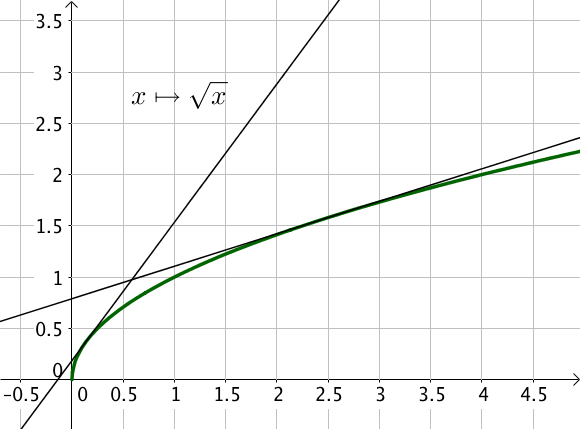
Par exemple, la fonction $y= \sqrt{x}$ est concave sur $\mathbb{R}^+_*$
Convexité des fonctions de référence
Convexité des fonctions de référence
Il s’agit d’apprendre parmi les fonctions usuelles lesquelles sont convexes et lesquelles sont concaves.
1) Fonctions convexes
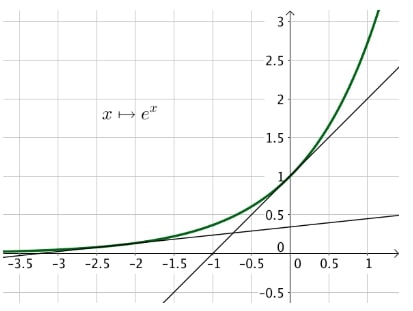
Les fonctions $x \mapsto x^2$ et $x \mapsto e^x$ sont des fonctions convexes sur $\mathbb{R}$.
Fonction exponentielle :
En effet, en reprenant la définition d’une fonction convexe, on peut vérifier que les courbes représentatives de ces deux fonctions sont au-dessus de chacune de leurs tangentes.
2) Fonctions concaves
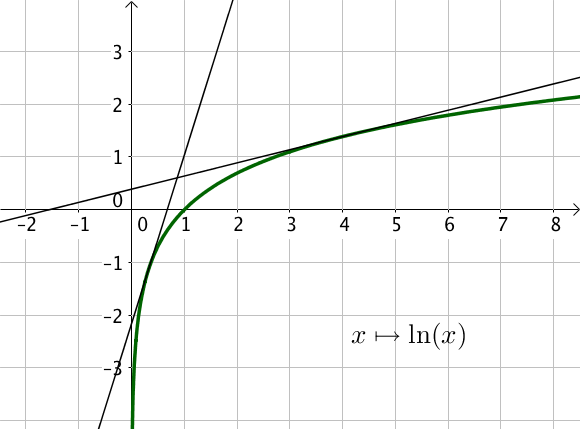
Les fonctions $x \mapsto \sqrt{x}$ et $x \mapsto \ln(x)$ sont des fonctions concaves sur $\mathbb{R}^+_*$.
La fonction racine carrée n’est pas dérivable en $0$, or la notion de convexité nécessite la dérivabilité de la fonction sur l’intervalle d’étude, donc la fonction racine carrée est uniquement concave sur $]0; +\infty [$.
On peut à nouveau vérifier graphiquement que les courbes sont en dessous de leurs tangentes.
Étude de la convexité d'une fonction
Étude de la convexité d’une fonction
Il existe deux principaux théorèmes permettant d’étudier l’éventuelle convexité ou concavité d’une fonction.
Théorème 1 :
Soit $f$ une fonction dérivable sur $I$,
1) $f$ est convexe sur $ I \ \iff \ f’$ est croissante sur $I$
2) $f$ est concave sur $ I \ \iff \ f’$ est décroissante sur $I$
Pour étudier la convexité d’une fonction, il suffit d’étudier les variations de sa dérivée.
Exemple :
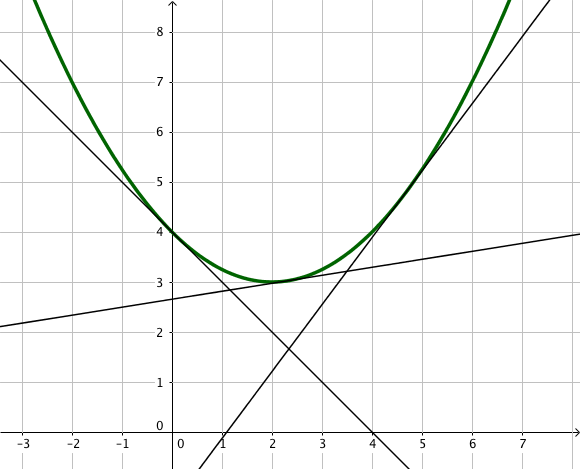
Etudions la fonction $f(x) = x^2 -3x +2$ sur l’intervalle $I = \mathbb{R}$.
$f$ est une fonction polynôme, elle est donc dérivable sur $\mathbb{R}$ et $\ f'(x) = 2x – 3$.
La dérivée de $\ f$ est une fonction affine. Le cours permet de conclure que $\ f’$ est croissante car $2>0$.
Ainsi, comme $\ f’$ est croissante sur $I$, $f$ est convexe sur $I$.
Théorème 2 :
Soit $f$ une fonction dérivable sur $I$ et on suppose de plus que $\ f”$ existe sur $I$ ($f”$ est la dérivée de la dérivée : c’est la dérivée seconde de $f$),
1) si pour tout $x \in I, \ f”(x) \geq 0$, alors $\ f$ est convexe sur $I$
2) si pour tout $x \in I, \ f”(x) \leq 0$, alors $\ f$ est concave sur $I$
Ces deux théorèmes sont liés.
En effet, si on suppose que $\ f”(x) \geq 0$, cela implique que $\ f’$ est croissante et dans les deux cas, $f$ est convexe.
Exemple :
Soit $f(x) = x^2$, on veut démontrer que $f$ est convexe sur $\mathbb{R}$.
Soit $x \in \mathbb{R}$, on calcule dans un premier temps $\ f'(x) = 2x$ puis la dérivée seconde $\ f”(x) = 2 \geq 0$.
Ainsi, pour tout $x \in \mathbb{R}, \ f”(x) \geq 0$, donc $f$ est convexe sur $\mathbb{R}$.
Point d'inflexion
Point d’inflexion
Définition
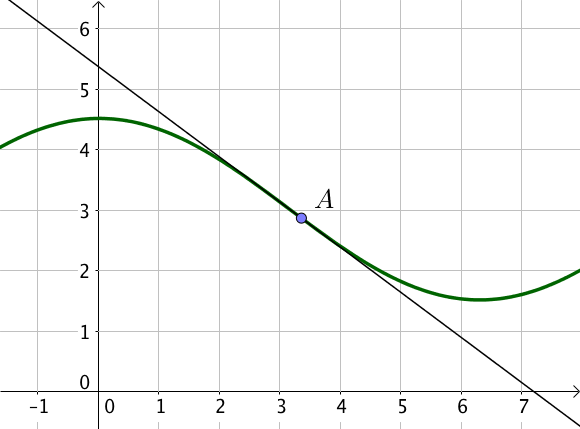
Un point d’inflexion d’une courbe est un point où la courbe traverse sa tangente.
Il s’agit d’une définition visuelle.
L’exemple qui suit représente un point d’inflexion au point $A$ car la courbe traverse sa tangente au point $A$ : elle est d’abord en dessous de sa tangente qui croise sa tangente au point $A$ et passe au dessus ensuite.
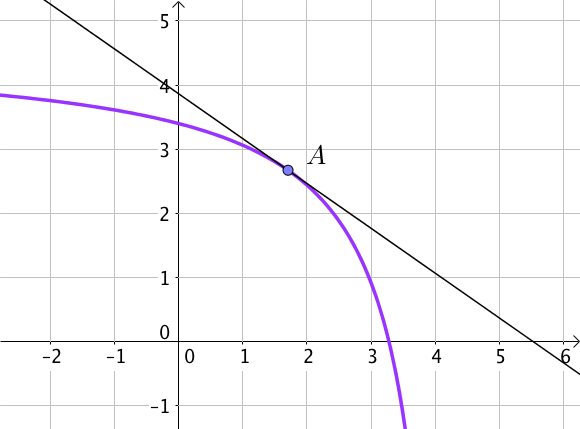
L’exemple ci-dessous montre que $A$ n’est pas un point d’inflexion : la courbe ne traverse pas sa tangente au point $A$ et reste toujours en dessous de cette dernière.
Exemple à connaitre :
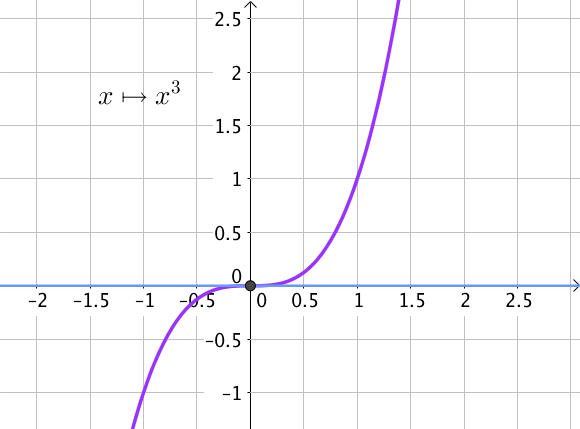
Parmi les fonctions usuelles, une fonction possède un point d’inflexion et constitue un exemple classique : c’est la fonction cube.
O l’origine du repère est un point d’inflexion.
En effet, pour $x \in \mathbb{R}, f'(x) = 3x^2$ donc $f'(0) = 0$.
De plus, la courbe traverse la tangente en ce point donc O est bien un point d’inflexion.
Étude de la continuité d'une fonction
Étude de la continuité d’une fonction
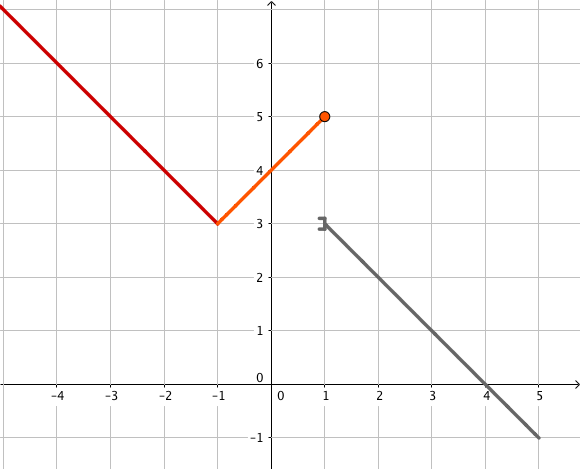
On souhaite étudier la continuité de la fonction définie par
$f(x) = \left \{ \begin{array}{l} -x + 2 \text{ si } x \leq -1 \\ x + 4 \text{ si } -1 < x \leq 1 \\ -x + 4 \text{ si } 1 < x \leq 5 \end{array} \right.$.
Il s’agit d’une fonction définie par morceaux car elle est définie sur différents intervalles.
On trace la fonction sur les différents intervalles.
On peut calculer l’image de $-1$ par la fonction $f$ sur l’intervalle $]-\infty, -1]$, on a ainsi $f(-1) = 3$.
On calcule également $f(-3) = 5$.
Comme $f$ est une fonction affine sur cet intervalle, on relit les deux points pour former une demi droite, car on s’arrête en $x = -1$, la formule $f(x) = -x + 2$ n’est vraie que pour $x \leq -1$.
On trace ensuite la fonction $f$ sur l’intervalle $]-1; 1]$. On ne peut pas calculer l’image de $-1$ par la fonction $f(x) = x + 4$.
On calcule alors $f(0) = 4$ et $f(1) = 5$ puis on relit ces deux points, pour former un segment dont les extrémités coïncident avec les points d’intersections avec les droites $x = -1$ et $x = 1$.
On trace de même la courbe représentative de $f$ sur le dernier intervalle.
On trace à l’extrémité gauche de la courbe ainsi tracée un crochet ouvert pour indiquer que l’image par $f$ de $x = 1$ ne se lit par sur cette troisième courbe mais sur la précédente.
On étudie maintenant la continuité de la fonction $f$.
Une fonction est continue lorsque l’on peut tracer la courbe représentative de la fonction sans lever le crayon.
Ainsi, $f$ est continue pour $x < 1$.
Graphiquement, on remarque que $f$ n’est pas continue en $x = 1$ car il faut lever le crayon.
Donc, $f$ est continue sur $]-\infty; 1[ \cup ]1; 5]$.
On souhaite désormais prouver que $f$ n’est pas continue en $x = 1$.
On calcule donc dans un premier temps la limite à gauche de $f$ en $1$, c’est à dire on calcule
$\lim \limits_{\substack{x \rightarrow 1 \\ x < 1}} f(x) = \lim \limits_{\substack{x \rightarrow 1 \\ x < 1}} x + 4$ car on regarde la fonction $f$ pour $x < 1$.
Ainsi, $\lim \limits_{\substack{x \rightarrow 1 \\ x < 1}} f(x) = 5$.
On calcule ensuite la limite à droite de $f$ en $1$, c’est à dire par valeur supérieure. On calcule donc :
$\lim \limits_{\substack{x \rightarrow 1 \\ x > 1}} f(x) = \lim \limits_{\substack{x \rightarrow 1 \\ x > 1}} – x + 4 = 3$.
On observe ainsi que la limite à gauche de $f$ en $1$ vaut $5$ et à droite vaut $3$ : ces deux limites étant différentes, la fonction n’est pas continue en $x = 1$.
Outil pour trouver un point d'inflexion
Outil pour trouver un point d’inflexion
Théorème :
Soit $f$ une fonction définie sur $]a; b[$ telle que $f”$ existe sur $]a; b[$ et $x_0$ un point de l’intervalle $]a; b[$,
si $f”$ s’annule en $x_0$, en changeant de signe alors le point $M_0(x_0, f(x_0))$ est un point d’inflexion.
Exemple :
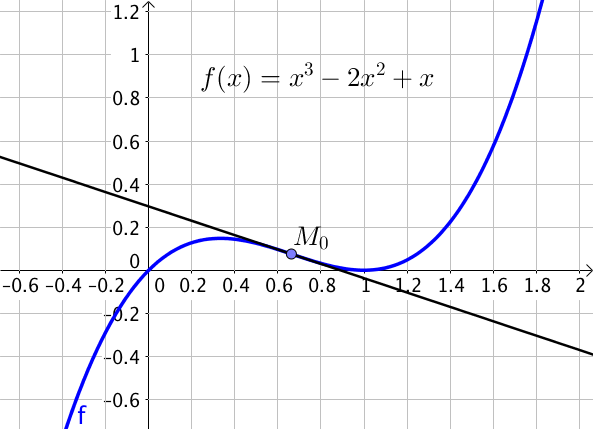
Soit $f$ la fonction définie par
$f(x) = x^3 – 2x^2 + x$ pour tout réel $x$,
on cherche d’éventuels points d’inflexion.
Pour cela, on calcule tout d’abord $f’$ qui existe car $f$ est polynomiale.
Pour tout $x \in \mathbb{R}, \ f'(x) = 3x^2 – 4x + 1$.
De même, $f’$ est dérivable sur $\mathbb{R}$ car c’est une fonction polynomiale : $f”$ existe donc et
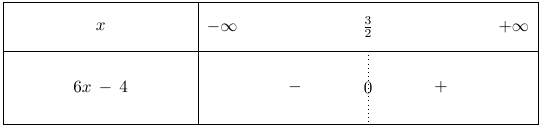
$f”(x) = 6x – 4$.
Pour trouver un point d’inflexion, on cherche à présent une valeur de $x$ pour laquelle la dérivée seconde s’annule et change de signe.
Soit $x \in \mathbb{R}, \ f”(x) = 0 \iff 6x – 4 = 0 \iff x = \dfrac{4}{6} \iff x = \dfrac{2}{3}$.
La dérivée s’annule donc en $x = \dfrac{2}{3}$.
On dresse alors le tableau de signe de $f”(x)$ pour tout réel $x$.
Ainsi, la dérivée seconde s’annule et change de signe en $x = \dfrac{2}{3}$.
Ainsi, $f$ admet un point d’inflexion en $x = \dfrac{2}{3}$.