L’incontournable du chapitre

Modules et arguments

Module et argument

Module

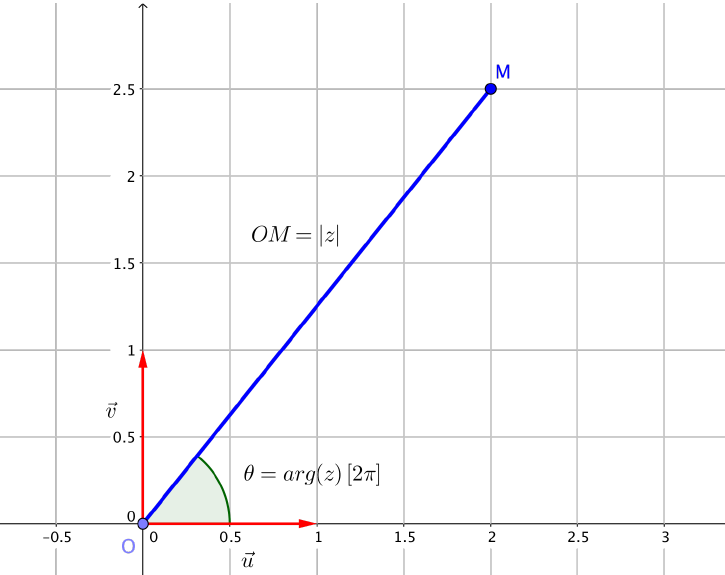
On considère un nombre complexe $z=a+ib$ et on note $M$ le point du plan complexe d’affixe $z$.

On définit le module de $z$ (qu’on note $|z|$) par la distance du point $M$ au point d’origine $O$.

On a alors la formule suivante :

$|z|=OM =\sqrt{a^2+b^2}$

Argument

On note $\overrightarrow{u}$ le vecteur directeur de norme $1$ de l’axe des réels.

On définit alors l’argument d’un nombre complexe $z=a+ib$ (affixe du point $M$ dans le plan complexe) l’angle formé par le vecteur $\overrightarrow{u}$ et le vecteur $\overrightarrow{OM}$.

On écrit alors :

$ \operatorname{arg} (z) = (\overrightarrow{u}, \overrightarrow{OM} ) ~ [2\pi]$

En notant $\theta = \operatorname{arg}(z)~ [2\pi]$ alors on a les égalités suivantes :

• $\cos(\theta)=\dfrac{a}{|z|}$
• $\sin(\theta)=\dfrac{b}{|z|}$

Illustration graphique

L’angle $\theta$ est ici un argument de $z$ : $\operatorname{arg}(z)=\theta ~ [2\pi]$.

Exemple

Calculer le module et un argument de $z_1=1+i$ et $z_2=4-4i$.

$z_1$ s’Ècrit : $z_1=a_1+ib_1$ avec $a_1=1$ et $b_1=1$ donc

$|z_1|=\sqrt{a_1^2+b_1^2}= \sqrt2$.

On note $\operatorname{arg}(z_1)=\theta_1 ~ [2\pi]$.

On a :

$\cos(\theta_1)=\dfrac{1}{\sqrt2}=\dfrac{\sqrt2}{2}$ et $\sin(\theta_1)$

$\cos(\theta_1)= \dfrac{1}{\sqrt2}=\dfrac{\sqrt2}{2}$.

Conclusion : $\theta_1=\dfrac{\pi}{4}~ [2\pi]$.

$z_2$ s’écrit : $z_2=a_2+ib_2$ avec $a_2=4$ et $b_2=-4$ donc

$|z_2|=\sqrt{a_2^2+b_2^2}=$

$|z_2|=\sqrt{16+16}=4\sqrt{2}$.

On note $\operatorname{arg}(z_2)=\theta_2 ~ [2\pi]$.

On a :

• $\cos(\theta_2)=\dfrac{4}{4\sqrt{2}}=\dfrac{\sqrt2}{2} $ 
• $\sin(\theta_2)= \dfrac{-4}{4\sqrt{2}}=-\dfrac{\sqrt2}{2}$.

Conclusion : $\theta_2=-\dfrac{\pi}{4}~ [2\pi]$.

Argument et angle formé par deux vecteurs

A savoir par coeur :

Soient \(A(z_A), B(z_B), C(z_C), D(z_D)\) quatre points d’un plan complexe.

\(arg \left(\dfrac{z_D – z_C}{z_B – z_A}\right) = (\overrightarrow{AB} ; \overrightarrow{CD}) [2\pi]\)

Ainsi \( arg \left(\dfrac{z_D – z_C}{z_B – z_A}\right)\) est égal à l’angle formé entre les vecteurs \(\overrightarrow{AB}\) et \(\overrightarrow{CD}\) modulo \(2\pi\).

Caractérisation de nombres complexes

Caractérisations des nombres complexes

Réels et imaginaires purs

Soit $z=a+ib$ un nombre complexe quelconque.

On dit que $z$ est réel lorsque $b=0$ et que $z$ est imaginaire pur lorsque $a=0$.

Exemple

• $2i$ est imaginaire pur,
• $3$ est réel
• $3+2i$ n’est ni réel, ni imaginaire pur.

Caractérisation avec les parties réelles et imaginaires

On constate simplement que si $z$ est un nombre complexe non nul, $\boxed{z\in \mathbb{R} \Leftrightarrow Im(z)=0}$.

Autrement dit, $z$ est réel si et seulement si sa partie imaginaire est nulle.

De même, $z$ est imaginaire pur si et seulement si sa partie réelle est nulle : $\boxed{z\in i\mathbb{R} \Leftrightarrow Re(z)=0}$.

Caractérisation avec l’argument

Soit $z$ un nombre complexe non nul.

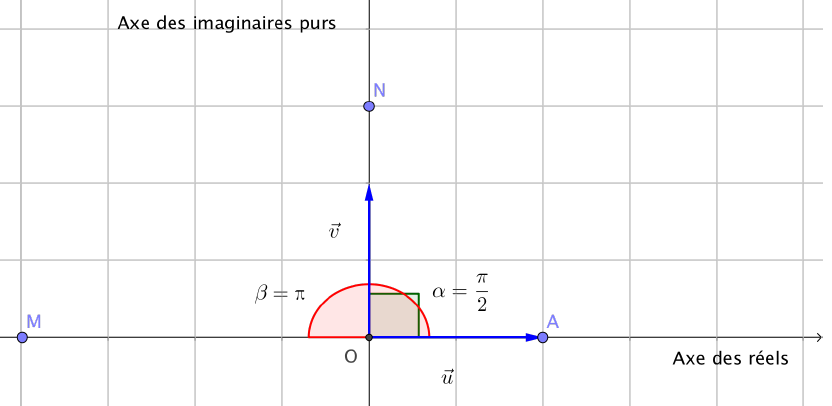
 $\bullet$ $z$ est réel si et seulement si $arg(z)=k\pi$ avec $k\in \mathbb{Z}$.

 $\bullet$ $z$ est imaginaire pur si et seulement si $arg(z)=\dfrac{\pi}{2}+k\pi$ avec $k\in \mathbb{Z}$.

Illustration graphique

L’affixe du point $M$ est un réel négatif, tandis que l’affixe du point $N$ est imaginaire pur.

le point $A$ a un affixe réel égal à $1$.

Propriétés des modules et arguments

Propriétés des modules et arguments

Module

Soient $z$ et $z’$ deux nombres complexes (avec $z’$ non nul).

On a les propriétés suivantes :

$\bullet $ $|z\times z’|=|z|\times |z’| $

$\bullet $ $ |z^n|=|z|^n$ pour $n\in \mathbb{N}$

$\bullet$ $\left| \dfrac{z}{z’}\right| = \dfrac{|z|}{|z’|}$ si $z’\neq 0$

$\bullet$ $|z+z’| \leqslant |z|+|z’|$

Argument

Soient $z$ et $z’$ deux nombres complexes (avec $z’$ non nul).

On a les propriétés suivantes :

$\bullet $ $ arg(z\times z’)=arg(z)+arg(z’) ~ [2\pi]$

$\bullet $ $ arg(z^n)=n\times arg(z) ~ [2\pi]$ pour $n\in \mathbb{N}$

$\bullet$ $ arg\bigg(\dfrac{z}{z’}\bigg) = arg(z)-arg(z’) ~ [2\pi]$

Exemple

Soient $a=1+i$ et $b=2i$ deux nombres complexes.

Calculer le module de $a^4$ ainsi qu’un argument de $\dfrac{a}{b}$.

D’après les propriétés du module on a : $|a^4|=|a|^4$ donc on calcule $|a|=\sqrt{1^2+1^2}=\sqrt2$.

Finalement : $|a^4|=|a|^4=\sqrt2^4= 4$.

D’après les propriétés des arguments, on a : $arg\left(\dfrac{a}{b} \right)= arg(a)-arg(b)~ [2\pi]$.

Ici, on a : $a={\sqrt2}\left(\dfrac{\sqrt2}{2}+i\dfrac{\sqrt2}{2}\right)$ donc $arg(a)=\dfrac{\pi}{4}~ [2\pi]$.

De plus, comme $b$ est un imaginaire pur, $arg(b)=\dfrac{\pi}{2}~ [2\pi]$.

On en déduit que $arg\left(\dfrac{a}{b} \right)=\dfrac{\pi}{4}-\dfrac{\pi}{2}~ [2\pi]$.

Finalement : $arg\left(\dfrac{a}{b} \right)= -\dfrac{\pi}{4} ~ [2\pi]$

Forme trigonométrique et exponentielle - Propriétés

Propriétés des formes trigonométriques et exponentielles

Opérations sur l’exponentielle complexe

Module

Par définition, on a $e^{i\theta}=\cos(\theta)+i\sin(\theta)$ donc

$|e^{i\theta}|=\sqrt{\cos^2(\theta)+\sin^2(\theta)}=1$. 

A retenir donc :Tout nombre complexe de la forme $e^{i\theta}$ se situe sur le cercle de centre $O$ et de rayon $1$, c’est-à-dire que son module vaut $1$.

Conjugué

Si $z=e^{i\theta}$ alors on a $\boxed{\bar z = e^{-i\theta}}$.

Périodicité et inverse

Les fonctions cosinus et sinus étant périodiques de période $2\pi$ on a, pour tout $k\in \mathbb{N}$ :

$\boxed{ e^{i(\theta+2k\pi)}=e^{i\theta}}$

On a, en outre, l’égalité suivante :

$\boxed{\dfrac{1}{e^{i\theta}}=e^{-i\theta}}$.

Produit et quotient

Si $\theta$ et un réel et $n$ un entier naturel, on a :

$\boxed{{(e^{i\theta})}^n=e^{in\theta}}$.

De manière plus générale, si $\theta$ et $\theta’$ sont des réels quelconques :

$\boxed{e^{i(\theta+\theta’)}=e^{i\theta}\times e^{i\theta’}}$.

Enfin, le quotient de deux exponentielles complexes donne le résultat suivant :

$\boxed{\dfrac{e^{i\theta}}{e^{i\theta’}}=e^{i(\theta-\theta’)}}$.

Exemple

On définit les deux nombres complexes $a=1+i$ et $b=2i$.

Calculer la forme exponentielle de $a$ puis de $b$ et en déduire celle de $a\times b$ et celle de $\dfrac{\bar a}{b}$.

En utilisant les méthodes vues dans les vidéos précédentes, on trouve aisément : 

$a=\sqrt2 e^{i\frac{\pi}{4}}$ et

$b=2e^{i\frac{\pi}{2}}$.

On en déduit avec les formules de la notation exponentielle que:

$a\cdot b = 2\sqrt2 e^{i(\frac{\pi}{2}+\frac{\pi}{4})} $

$a\cdot b = 2\sqrt2 e^{i\frac{3\pi}{4}}$

De même, on a :

$\bar a = \sqrt2 e^{-i\frac{\pi}{4}}$ donc

$\dfrac{\bar a}{b}= \dfrac{\sqrt2}{2}e^{i(-\frac{\pi}{4}-\frac{\pi}{2})}$

$\dfrac{\bar a}{b}= \dfrac{\sqrt2}{2}e^{-i\frac{3\pi}{4}}$.