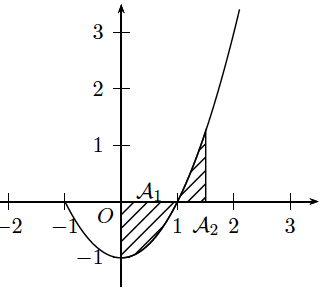Définition de l'intégrale
Définition de l’intégrale
Définition
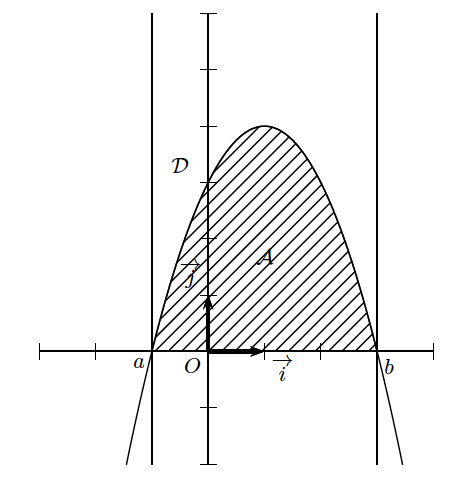
Soit (O,$\overrightarrow {i}$,$\overrightarrow {j}$) un repère orthonormé et une fonction $f$ continue et positive sur un intervalle $[a,b]$.
$\mathcal{D}$ est le domaine du plan délimité par $x$=$a$ , $x$=$b$, l’axe des abscisses et $\mathcal{C}_f$, la courbe représentative de la fonction $f$.
L’intégrale de $f$ sur $[a,b]$ notée $ \displaystyle \int \limits_a^b f (t)dt$ est l’aire $\mathcal{A}$ du domaine $\mathcal{D}$ exprimée en unités d’aire.
Exemple
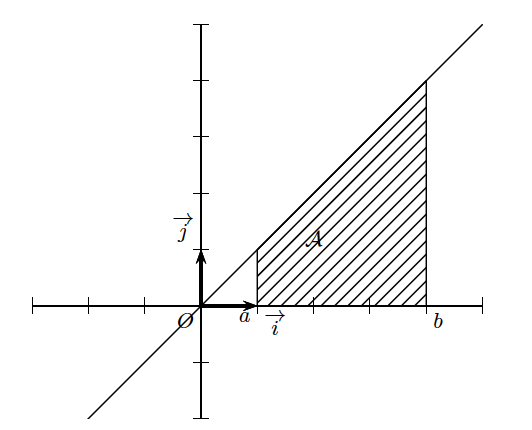
Calculer $I = \displaystyle \int_{1}^4 x dx = \int_{1}^4 t dt$ ($x$ et $t$ sont des variables muettes).
Etape 1 : On repère l’aire recherchée.
Etape 2 : On remarque qu’il s’agit d’un trapèze rectangle.
Etape 3 : La formule du calcul d’aire du trapèze rectangle est connue. On peut l’utiliser pour calculer l’intégrale :
$ A = \dfrac{(B + b) \times h}{2}$
$ A = \dfrac{5 \times 3}{2}$
Finalement, $I = \dfrac{15}{2}$ (exprimée en unité d’aire)
Cas d’une fonction non positive
Le signe d’une aire est toujours positif en revanche celui d’une intégrale va dépendre de la position de la courbe par rapport à l’axe des abscisses.
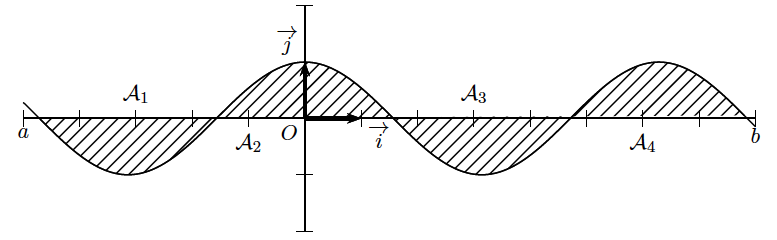
Ainsi, on pourrait avoir $I$:
$I= \displaystyle \int \limits_a^b f (t)dt=- \mathcal {A}_1+ \mathcal {A}_2-\mathcal {A}_3+\mathcal {A}_4$
Les $ \mathcal A_{i}$ sont les aires respectives des quatre domaines representés sur le graphique.
Exemple
Voici comment représenter: $\displaystyle \int \limits_0^{1,5} (x^2 -1)dx$
$I = \displaystyle \int \limits_0^{1,5} (x^2 -1)dx =- \mathcal {A}_1+ \mathcal {A}_2$
Relation de Chasles
Relation de Chasles.
Convention
\(\displaystyle\int_{a}^a f(t)dt=0 \) et
\(\displaystyle\int_{a}^b f(t)dt= – \int_{b}^a f(t)dt\)
Propriété
Soit \(f \) une fonction continue sur un intervalle $I$. Pour tous réels $a$, $b$, $c$ de l’intervalle $I$, on a :
\(\displaystyle\int_{a}^c f(t)dt +\int_{c}^b f(t)dt =\int_{a}^b f(t)dt\)
Exemple
Réduire les expressions suivantes :
1. \(I = \displaystyle\int_{1}^2 (x^2 – 1) dx + \int_{1}^2 dx + \int_{2}^3 x^2 dx\)
2. \(J = \displaystyle\int_{0}^1 \frac{1}{1 + x^2} dx + \int_{-2}^0 \frac{1}{1 + x^2} dx \)
Correction
1. Etape 1 : On utilise la linéarité de l’intégrale pour regrouper les intégrales de mêmes bornes.
\(I = \displaystyle\int_{1}^2 (x^2 – 1+1) dx + \int_{2}^3 x^2 dx\)
\(I = \displaystyle\int_{1}^2 x^2 dx + \int_{2}^3 x^2 dx\)
Etape 2 : Les fonctions sont les mêmes et les bornes se suivent, on utilise la relation de Chasles.
\(I = \displaystyle\int_{1}^2 x^2 dx + \int_{2}^3 x^2 dx\)
\(I = \displaystyle\int_{1}^3 x^2 dx \)
2. Etape 1 : La fonction $g(x)=\dfrac{1}{1 + x^2}$ est définie et continue sur $[-2;1]$.
On place la seconde intégrale devant la première pour retrouver la propriété.
\(J = \displaystyle\int_{-2}^0 \frac{1}{1 + x^2} dx +\int_{0}^1 \frac{1}{1 + x^2} dx \).
Etape 2 : On peut ainsi utiliser la relation de Chasles.
\(J = \displaystyle\int_{-2}^1 \frac{1}{1 + x^2} dx \).
Les primitives
Primitive d’une fonction
Définition
Soit $f$ une fonction définie sur un intervalle $I$.
On dit qu’une fonction $F$ est une primitive de $f$ sur $I$ si et seulement si $F$ est dérivable sur $I$ et pour tout $x$ de $I$, $F'(x) = f(x)$.
Primitives usuelles
Opérations sur les primitives
Opérations élémentaires sur les primitives
Propriétés
Soit $u$ et $v$ deux fonctions dérivables sur un intervalle $I$ réel.
| Fonction | Une primitive | Conditions |
| $u’+v’$ | $u+v$ | |
| $ku’$ (avec $k$ constante) | $ku$ | |
| $u’u^n$ avec $n$ appartient à $\mathbb{Z}$ et différent de $-1$ | $\dfrac{u^{n+1}}{n+1}$ | $u$ différent de $0$ sur $I$ si $u\leq 0$ |
| $\dfrac{u’}{\sqrt u}$ | 2$\sqrt u$ | $u>0$ sur $I$ |
| $\dfrac{v’}{v^2}$ | $-\dfrac{1}{v}$ | $v\neq 0$ sur $I$ |
| $u’e^{u}$ | $e^{u}$ | |
| $\dfrac{u’}{u}$ |
$\ln(u)$ $\ln(-u)$ |
$u>0$ sur $I$ $u<0$ sur $I$ |
| $u'(v’\circ u)$ | $v\circ u$ |
Exemples
1. Chercher une primitive sur \(\mathbb{R}\) de : $ f(x) = x e^{x^2+ 1}$
2. Chercher une primitive sur \(\mathbb{R}\) de : $ g(x) = \dfrac{6x + 3}{x^2 + x + 1}$.
Correction
1. $ f(x) = x e^{x^2+ 1}$
Etape 1 : On cherche les expressions de \(u\) et \(u’\) pour arriver à la forme \(u’ e^u\).
\(u (x) = x^2+ 1 \) et \(u'(x)= 2x \)
Etape 2 : On multiplie par $2$ et par $\dfrac{1}{2}$ pour faire apparaître le “$2$” manquant.
$ f(x)=\dfrac{1}{2} \times 2x e^{x^2+ 1} $
$ f(x)=\dfrac{1}{2} u'(x) e^u(x) $
Etape 3 : On définit une primitive grâce au cours.
$ F(x)= \dfrac{1}{2} e^{x^2+ 1}$
2.$ g(x) = \dfrac{6x + 3}{x^2 + x + 1}$
Etape 1 : On note \(u(x)= x^2 + x + 1 \) et \(u'(x)=2x+1\). On factorise par $3$ le numérateur pour faire apparaître \(u'(x)\).
On a : $ g(x) = \dfrac{3(2x + 1)}{x^2 + x + 1}$.
Soit : $ g(x) = \dfrac{3u'(x)}{u(x)}$.
Etape 2 : On remarque que $x^2+x+1>0$ sur $\mathbb{R}$ et on définit une primitive de $g$ grâce au cours.
$ G(x) = 3\ln (x^2 + x + 1)+ c$
Calculs d'intégrales
Calculs d’intégrales
Propriété
Soit $f$ une fonction continue sur un intervalle $I$.
Soit $F$, une primitive de \(f\) sur $I$.
Pour tous réels $a$ et $b$ de l’intervalle $I$, on a :
$\displaystyle\int_{a}^b f(t) dt= F(b)- F(a) $ que l’on note aussi
$\displaystyle\int_{a}^b f(t) dt=\left[F(t)\right]_{a}^b$
Exemples
Calculer :
$I$=\(\displaystyle\int_{1}^2 \dfrac{x^2+3x+1}{x^2}dx\).
$J$=\(\displaystyle \int_{0}^1 x(2x^2-1)^3 dx\).
Correction
Calcul de $I$
Étape 1 : La fonction $f(x)= \dfrac{x^2+3x+1}{x^2}$ est définie et continue sur $[1;2]$.
On décompose l’expression en trois fractions de dénominateur commun.
$I$=\(\displaystyle\int_{1}^2 (\dfrac{x^2}{x^2}+\dfrac{3x}{x^2}+\dfrac{1}{x^2})dx\)
$I$=\(\displaystyle\int_{1}^2 (1+\dfrac{3}{x}+\dfrac{1}{x^2})dx\)
$I$=\(\displaystyle\int_{1}^2 dx+ \int_{1}^2\dfrac{3}{x}dx+ \int_{1}^2\dfrac{1}{x^2}dx\)
Étape 2 : On peut définir des primitives de chaque expression.
$I$= \(\displaystyle \left[x+3\ln x-\dfrac{1}{x}\right]_{1}^2\)
Étape 3 : On calcule $F(2)-F(1)$.
$I$= \(\displaystyle (2+3\ln 2-\dfrac{1}{2})-(1+3\ln 1-\dfrac{1}{1})\)
$I$= \(\displaystyle \dfrac{3}{2}+3\ln 2 \) (unité d’aire).
Calcul de $J$
On pose : $u(x)=2x^2-1$ et $u'(x)=4x$.
On modifie l’expression pour la faire apparaître sous la forme $u’\times u^3$.
$J$=\(\displaystyle \dfrac{1}{4} \int_{0}^1 4x(2x^2-1)^3 dx \)
$J$=\(\displaystyle \dfrac{1}{4}\left[\dfrac{1}{4}(2x^2-1)^4\right]_{0}^1 \)
$J$=\(\displaystyle \dfrac{1}{4}\left((\dfrac{1}{4}(1)^4)-(\dfrac{1}{4}(-1)^4)\right)\)
$J$=\(\displaystyle \dfrac{1}{4}\left(\dfrac{1}{4}-\dfrac{1}{4}\right)\)
$J$= $0$
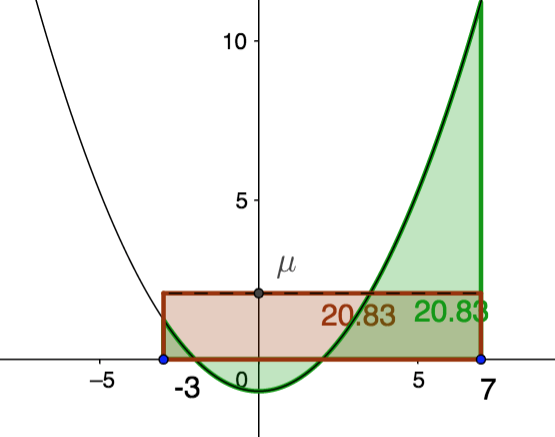
Valeur moyenne d'une fonction
Valeur moyenne d’une fonction
Définition
Soient $a$ et $b$ deux réels tels que $a < b$ et \(f\) est continue sur \([a,b]\).
On appelle valeur moyenne de \(f\) sur \([a,b]\), le nombre réel $\mu$ défini par :
\( \displaystyle \mu = \frac{1}{b-a} \int_{a}^b f(t)dt\)
Interprétation graphique
On peut déterminer la valeur de l’intégrale de $f$ en effectuant le produit en croix:
\( \displaystyle \mu (b-a)= \int_{a}^b f(t)dt = \mathcal{A}\)
Voici l’exemple de la fonction $f(x)=0,25x^2-1$ sur l’intervalle $[-3;7]$