Étude de la fonction cosinus
Etude de la fonction cosinus
Domaine de définition et dérivée
La fonction cosinus est définie sur $\mathbb{R}$.
Elle est, en outre, $2\pi$-périodique (ce qui signifie que pour tout $x\in\mathbb{R}, \cos(x+2\pi)=\cos(x)$)
et paire (pour tout $x\in\mathbb{R}, \cos(-x)=\cos(x)$) ce qui permet de restreindre son étude à $[0,\pi]$.
Son domaine de dérivabilité est $\mathbb{R}$ et pour tout $x\in\mathbb{R}, \cos'(x)=-\sin(x)$.
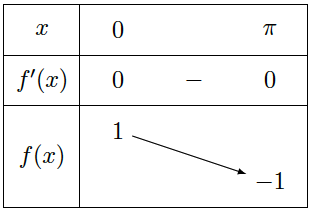
Variations sur $[0,\pi]$
Pour étudier les variations de la fonction cosinus, on étudie le signe de sa dérivée c’est-à-dire le signe de $-\sin(x)$ sur $[0,\pi]$.
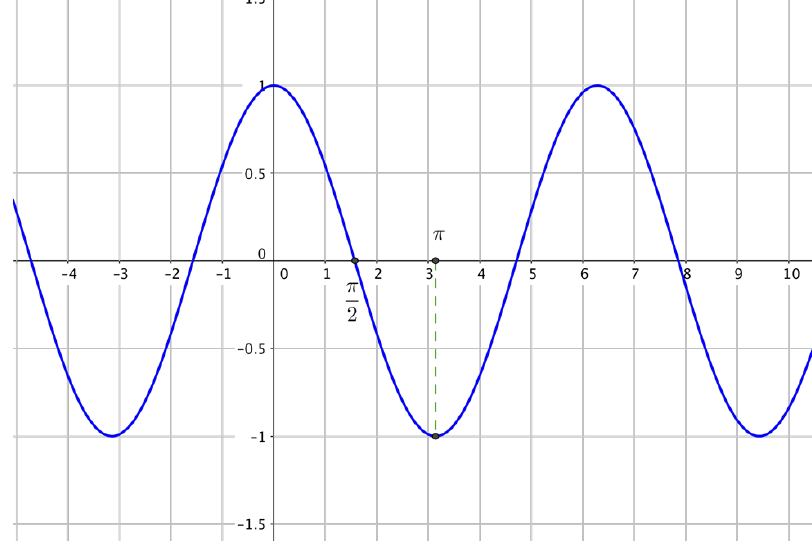
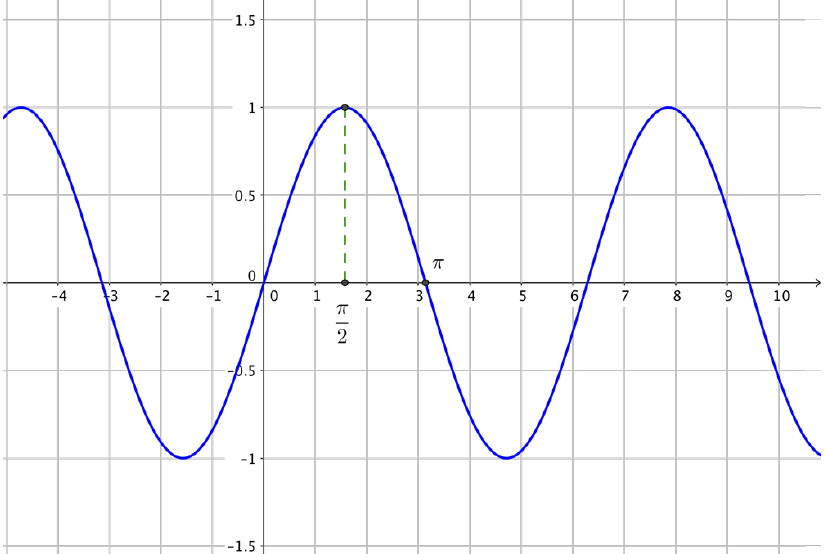
Représentation graphique
Courbe représentative de la fonction cosinus obtenue avec les propriétés de parité et de périodicité de la fonction:
Propriétés algébriques et autres formules
Pour tout $x\in\mathbb{R}$, $\cos^2(x)+\sin^2(x)=1$.
Pour tout $x\in\mathbb{R}$, $\cos(2x)=2\cos^2(x)-1$.
Pour tous $a,b$ réels, $\cos(a+b)=\cos(a)\cos(b)-\sin(a)\sin(b)$.
Formule d’Euler : $\cos(\theta)= \dfrac{e^{i\theta}+e^{-i\theta}}{2}$, où $e^{i\theta}$ est le nombre complexe de module 1 et
d’argument $\theta$ : $e^{i\theta}=\cos ({\theta}) +i\sin({\theta})$.
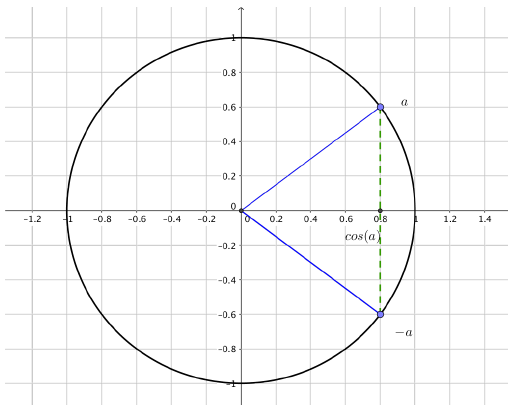
$\cos(-x) =\cos(x)$
$\cos(x+\pi)= -\cos(x)$
$\cos(\frac{\pi}{2}-x)= \sin(x)$
Propriétés de la fonction cosinus
Propriétés de la fonction Cosinus
On pose pour \(x \in \mathbb{R}\), \(f(x) = \cos x\).
1) On a \( \cos (x + 2\pi) = \cos x\)
Soit \(f(x + 2\pi) = f(x)\).
On dit que \(f\) est \(2\pi\) périodique.
Conséquence : On peut tracer la courbe uniquement sur un intervalle de longueur \(2\pi\).
2) On a \(\cos (-x) = \cos x\).
Soit \(f(-x) = f(x)\).
La fonction est paire.
Conséquence : La courbe est symétrique par rapport à l’axe des ordonnées.
Étude de la fonction sinus
Etude de la fonction sinus
Domaine de définition et dérivée
La fonction sinus est définie sur $\mathbb{R}$.
Elle est impaire (pour tout $x\in\mathbb{R}, \sin(-x)=-\sin(x)$) et $2\pi$-périodique (pour tout $x\in\mathbb{R}, \sin(x+2\pi)=\sin(x)$) ce qui permet de restreindre son étude à $[0,\pi]$.
Son domaine de dérivabilité est $\mathbb{R}$ et pour tout $x\in\mathbb{R}, \sin'(x)=\cos(x)$.
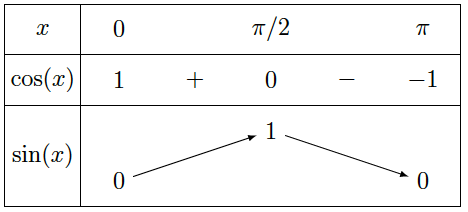
Variations sur $[0,\pi]$
Pour étudier les variations de la fonction sinus, on étudie le signe de sa dérivée c’est-à-dire le signe de $\cos(x)$ sur $[0,\pi]$.
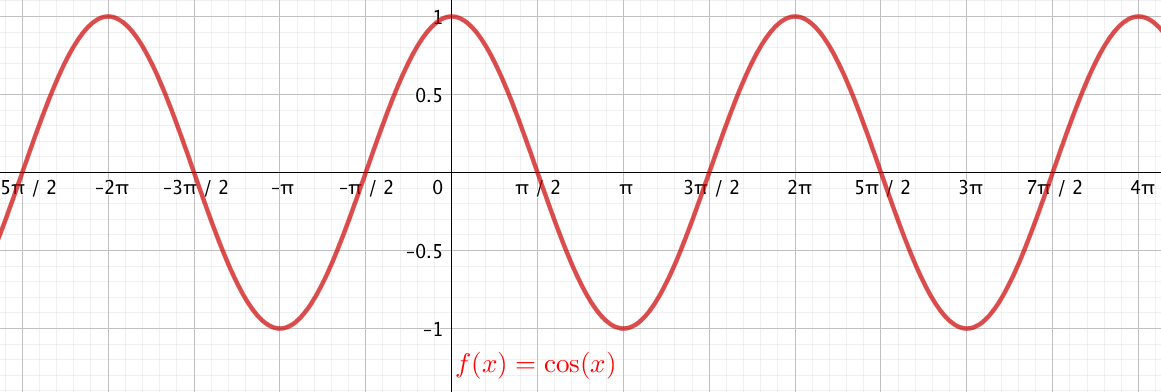
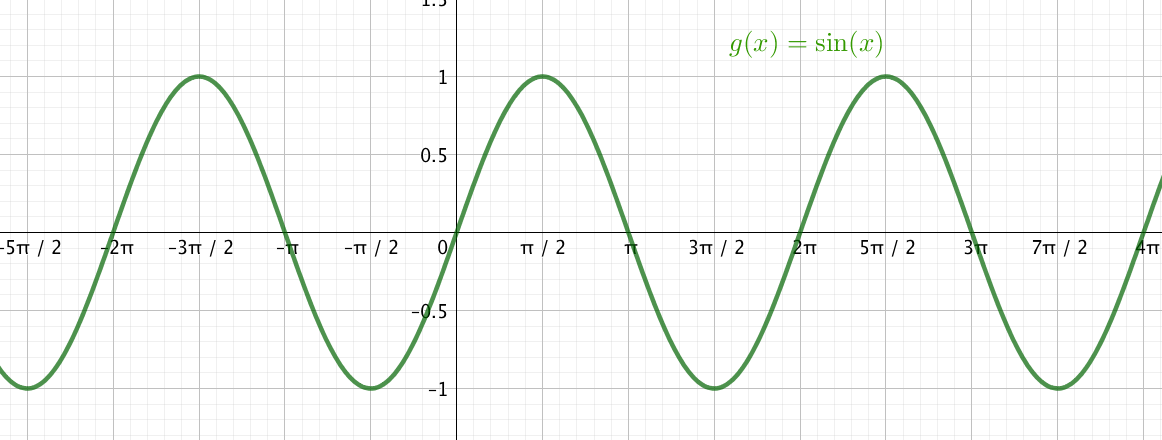
Représentation graphique
Courbe représentative de la fonction sinus obtenue avec les propriétés de parité et de périodicité de la fonction :
Propriétés algébriques et autres formules
Pour tout $x\in\mathbb{R}$, $\cos^2(x)+\sin^2(x)=1$.
Pour tout $x\in\mathbb{R}$, $\sin(2x)=2\cos(x)\sin(x)$
Pour tous $a,b$ réels, $\sin(a+b)=\cos(a)\sin(b)+\cos(b)\sin(a)$.
Formule d’Euler : $\sin(\theta)= \dfrac{e^{i\theta}-e^{-i\theta}}{2i}$.
$\sin(-x)=-\sin(x)$
$\sin(x+\pi)= -\sin(x)$
$\sin(\frac{\pi}{2}-x)= \cos(x)$
Propriétés de la fonction sinus
Propriétés de la fonction Sinus
On pose, pour \(x \in \mathbb{R}\), \(f(x) = \sin \ x\)
1) On a \( \sin (x+2 \pi) = \sin \ x\)
Soit \( f (x+2 \pi) = f (x)\)
On dit que \(f\) est \(2\pi\) périodique.
Conséquence : On peut tracer la courbe uniquement sur un intervalle de longueur \(2\pi\).
2) On a \( \sin (-x) = \sin \ x\)
Soit \( f (-x) = -f (x)\)
La fonction \(f\) est impaire.
Conséquence : La courbe est symétrique par rapport à l’origine \(O\) du repère.
Calculs de limites de fonctions trigonométriques
Calculs de limites de fonctions trigonométriques
Limites au voisinage de l’infini
Les fonctions cosinus et sinus n’ont pas de limite en $+\infty$ ni en $-\infty$.
Cependant, on peut comparer leurs croissances aux puissances de $x$ :
$\displaystyle \lim_{x\to \pm \infty} \dfrac{\cos(x)}{x^n}=0$ avec $n\in \mathbb{N}^\star$
$\displaystyle \lim_{x\to \pm \infty} \dfrac{\sin(x)}{x^n}=0$ avec $n\in\mathbb{N}^\star$
Ces résultats s’obtiennent très facilement avec le théorème des gendarmes
Limite en $0$
En faisant apparaître un taux de variation, on montre que :
${\displaystyle\lim_{x\to 0}\dfrac{\sin(x)}{x}=1}$
Preuve :
$\displaystyle\lim_{x\to 0} \dfrac{\sin(x)}{x}=\lim_{x\to 0}\dfrac{\sin(x)-\sin(0)}{x-0} =\sin'(0) = \cos(0) = 1$
Exemple
Calculer la limite en $0$ de la fonction $f(x)=\dfrac{\sin(4x)}{x}$.
Il s’agit ici de faire apparaître un taux de variation pour pouvoir calculer cette limite qui est une forme indéterminée du type : $\dfrac00$.
Pour cela, on écrit $f(x) = 4 \times \dfrac{\sin(4x)}{4x}$.
Or, on sait que $\displaystyle\lim_{x\to 0}\dfrac{\sin(x)}{x}=1$ et si le nombre $x$ tend vers $0$ alors $4x$ tend aussi vers $0$.
Ainsi : $\displaystyle \lim_{x\to 0}\dfrac{\sin(4x)}{4x}=1$.
En multipliant par la constante $4$, on en déduit finalement la limite de $f$ en $0$ :
${\displaystyle\lim_{x\to 0}f(x)=4}$
Dérivation des fonctions trigonométriques
Dérivation de fonctions trigonométriques
Propriétés
Soient $a$ et $b$ deux réels.
Pour tout $x\in \mathbb{R},$
$(\cos(ax+b))’=-a\sin(ax+b)$
$(\sin(ax+b))’=a\cos(ax+b)$
En particulier, pour $a=1$ et $b=0$,
Pour tout $x\in \mathbb{R},$
$(\cos(x))’=-\sin(x) $
$(\sin(x))’=\cos(x) $
Exemples
Dériver les fonctions suivantes en précisant leurs ensembles de dérivabilité :
1) $f(x)=\dfrac{\sin(x)}{\cos(x)}$ sur $\left] -\dfrac{\pi}{2},\dfrac{\pi}{2} \right[$
2) $g(x) = \dfrac{\sin(3-2x)}{2}$ sur $\mathbb{R}$
3) $k(x)= \sin(x)\cos(x)$ sur $\mathbb{R}$
Correction
1) $f$ est dérivable sur $\left] -\dfrac{\pi}{2},\dfrac{\pi}{2} \right[$ en tant que quotient de fonctions dérivables sur $\left] -\dfrac{\pi}{2},\dfrac{\pi}{2} \right[$ avec $\cos(x)$ non nul sur cet intervalle.
On écrit $u(x)=\sin(x)$ et $v(x)=\cos(x)$ de sorte que $f(x)=\dfrac{u(x)}{v(x)}$.
On a alors $u'(x)=\cos(x)$ et $v'(x)=-\sin(x)$ et pour tout $x\in \left] -\dfrac{\pi}{2},\dfrac{\pi}{2} \right[$ :
$ f'(x) = \dfrac{u'(x)v(x)-u(x)v'(x)}{v^2(x)}$
$f'(x)= \dfrac{\cos^2(x)+\sin^2(x)}{\cos^2(x)}$
$f'(x)=\dfrac{1}{\cos^2(x)}$
2) Pour $x\in\mathbb{R}$ :
$ g'(x) = -2\cos(3-2x)\times \dfrac12$
soit $ g'(x) = -\cos(3-2x)$
3) $k$ est dérivable sur $\mathbb{R}$ en tant que produit de fonctions dérivables sur $\mathbb{R}$.
On écrit $u(x)=\cos(x)$ et $v(x)=\sin(x)$ de sorte que $k(x)=u(x)v(x)$
On a alors : $u'(x)=-\sin(x)$ et $v'(x)=\cos(x)$.
Ainsi, pour $x\in\mathbb{R}$ :
$ k'(x) = u'(x)v(x)+u(x)v'(x)$
$ k'(x)=-\sin^2(x)+\cos^2(x) $
$ k'(x)= 2\cos^2(x)-1$
$ k'(x)=\cos(2x)$
Équations trigonométriques
Equations trigonométriques
Egalité de cosinus ou de sinus
Conditions d’égalité de deux cosinus :
$ \cos(x)=\cos(a) \Leftrightarrow x=a+2k\pi \text{ ou } x=-a+2k\pi \text{ avec } k\in \mathbb{Z}$
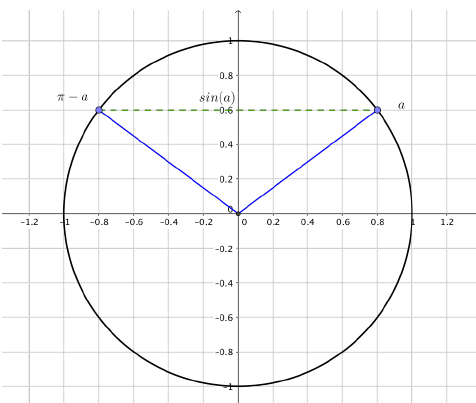
Conditions d’égalité de deux sinus :
$\sin(x)=\sin(a) \Leftrightarrow x=a+2k\pi \text{ ou } x=(\pi-a)+2k\pi \text{ avec } k\in\mathbb{Z}$
Exemple
Résoudre dans $\mathbb{R}$ l’équation $\sin(3x)=\dfrac{\sqrt2}{2}$
On a $\dfrac{\sqrt2}{2}=\sin\left( \dfrac{\pi}{4}\right)$ d’après le cours, donc :
$\sin(3x)=\dfrac{\sqrt2}{2} \Leftrightarrow 3x=\dfrac{\pi}{4}+2k\pi$ ou $3x=\left(\pi-\dfrac{\pi}{4}\right)+2k\pi = \dfrac{3\pi}{4}+2k\pi $
C’est à dire :
$x=\dfrac{\pi}{12}+\dfrac{2k\pi}{3}$ ou $x=\dfrac{\pi}{4}+\dfrac{2k\pi}{3}$ avec $k\in\mathbb{Z}$