L’incontournable du chapitre

Probabilité de l'événement contraire

Probabilité de l’événement contraire

Définition et propriété

L’événement contraire de $A$ est l’événement constitué de toutes les issues qui ne sont pas dans $A$.

Il se note $\overline{A}$. 

On a: $ \boxed{ p(\overline{A}) = 1-p(A)}$

Exemple

Une enquête est effectuée auprès de 300 jeunes, deux ans après l’obtention de leur baccalauréat : 70 sont au chômage.

On choisit un jeune au hasard.

On note $C$ =”le jeune choisi est au chômage”.

Calculer la probabilité que le jeune choisi ne soit pas au chômage.

• étape 1 : On reconnaît dans l’énoncé l’expression clé qui nous indique l’événement contraire, ici la négation.

$\overline{C}$ = ” le jeune choisi n’est pas au chômage “

• étape 2 : On applique la formule du cours sur la probabilité de l’événement contraire :

$p(\overline{C}) = 1-p(C)$

$p(\overline{C}) = 1- \dfrac{70}{300}$

• étape 3 : Attention à bien simplifier les résultats sous forme fractionnaire ou avec une valeur approchée.

$p(\overline{C}) = 1- \dfrac{7}{30}$

$p(\overline{C}) = \dfrac{23}{30}$

$p(\overline{C}) \approx 0,77$

Probabilités conditionnelles

Probabilités conditionnelles

Si deux événements sont dépendants plutôt qu’indépendants, comment calculer la probabilité que les deux se réalisent, puisque la probabilité de réalisation de l’un dépend de la réalisation de l’autre ?

Il nous faut connaître pour cela le degré de dépendance des deux événements qui est indiqué par la notion de probabilité conditionnelle.

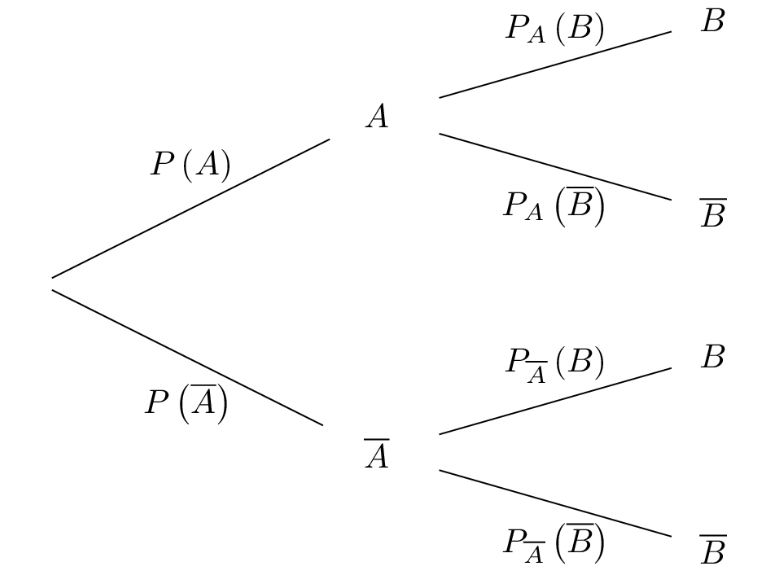
Définition

Soient $A$ et $B$ deux événements, $B$ étant supposé de probabilité non nulle.

On appelle probabilité conditionnelle de $A$ sachant $B$, la probabilité de réalisation de l’événement $A$ sachant que $B$ est déjà réalisé.

On la note :$P_B(A) = \dfrac{p(A\cap B)}{p(B)}$

$P_B(A)$ se lit “probabilité de $A$ si $B$” ou “probabilité  de $A$ sachant $B$” .

On représente souvent l’arbre suivant :

Exemple

Une entreprise fabrique des boulons destinés à l’industrie. On admet que 3% des boulons présentent un défaut et sont inutilisables. On contrôle les boulons fabriqués.
Ce contrôle refuse 95% des boulons avec défaut et accepte 92% des boulons sans défaut.
On choisit un boulon au hasard.
On note:

$D $ = “le boulon a un défaut”  

$A$ = “le boulon est accepté”

Que valent $P_D(\overline{A})$  et $P_{\overline{D}}(A)$ ?

On interprète chaque pourcentage présent dans l’énoncé sous forme de probabilité.

On traduit les probabilités conditionnelles présentes dans l’énoncé avec la notation appropriée.

$P_{D}(\overline{A})=0,95$

$P_{\overline{D}}(A)=0,92$.

Application des probabilités conditionnelles au calcul de $p(A\cap B)$

Pour tous événements $A$ et $B$ quelconques, on a :

$p(A\cap B) = p(B) \times \mathrm{p}_B(A)$ 

$p(A\cap B) = p(A) \times \mathrm{p}_A(B)$

Formule des probabilités totales

Formule des probabilités totales

Définition

Une partition de $\Omega$ est un ensemble de parties de $\Omega$ deux à deux disjointes et dont la réunion est $\Omega$.

Propriété

Si $B_1 , B_2\ldots,B_n$ forment une partition de $\Omega$, alors, pour tout événement $A$, on a:

$p(A)= p(A\cap B_1) + p(A\cap B_2)+\ldots + p(A\cap B_n)$

Exemple

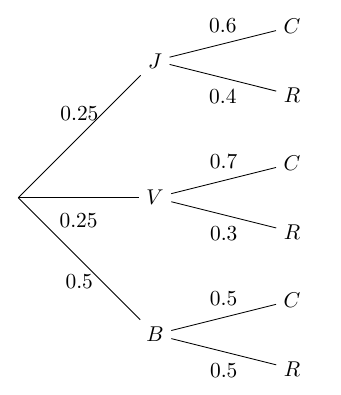
Un sac contient des jetons de 3 couleurs différentes : blancs (50%), verts (25%) et jaunes (25%).

Les jetons peuvent être ronds ou carrés.

La moitié des jetons blancs sont ronds, 70% des jetons verts sont carrés et 4 jetons jaunes sur 10 sont ronds.

On choisit un jeton au hasard. Quelle est la probabilité que le jeton soit rond ?

On note les événements :

$B$ : “Le jeton est blanc “.

$V$ : “Le jeton est vert “.

$J$ : “Le jeton est jaune “.

$R$ : “Le jeton est rond “.

$C$ : “Le jeton est carré “.

• étape 1 : On réalise un arbre de probabilité afin de mieux visualiser chaque situation.

• étape 2 : On remarque que les événements $B, V$ et $J$ forment une partition de l’univers (et il faut l’écrire !).
• étape 3 : On applique la formule des probabilités totales.

$p(R)= p(B\cap R) + p(J\cap R)+p(V\cap R)$

$p(R)= p(B)\times p_{B}(R) + p(J)\times p_{J}(R)+ p(V)\times p_{V}(R)$

$p(R)= 0,5\times 0,5 + 0,25 \times 0,3 + 0,25\times 0,4$

$p(R) = 0,425$

La probabilité que le jeton soit rond est égale à 0,425.

La loi binomiale

Loi binomiale

Les conditions de la loi binomiale :

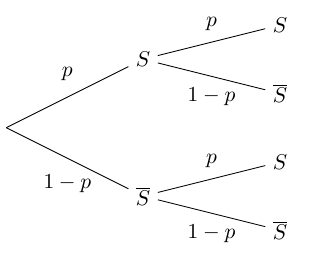
On considère une expérience aléatoire qui ne comporte que deux résultats :

• Le succès $S$ et
• l’échec $\overline{S}$ son événement contraire.

On pose :

$p=p(S)$

et $q=p(\overline{S}) =1-p(S)$ 

On répète $n$ fois l’expérience, les répétitions sont indépendantes.

Soit $X$ le nombre de succès au cours des $n$ répétitions.

On dit alors que $X$ suit la loi binomiale de paramètres $n$ et $p$.

On note cette loi $\mathcal{B}(n,p)$.

Exemple d’arbre pour $n=2$

La probabilité d’obtenir $k$ succès au cours des $n$ répétitions est donnée par la formule :

$p(X=k)= \displaystyle\binom{n}{k} p^k \times (1-p)^{n-k}$

Exemple

a) On lance 10 fois un dé bien équilibré. Quelle est la probabilité d’obtenir 4 fois le chiffre 1 au cours des 10 lancers 

b) Quelle est la probabilité d’obtenir au moins une fois le chiffre 1 au cours des 10 lancers ?

a) D’après la calculatrice, on a :

$p(X=4)\approx 0,054$

b) Pour s’éviter de longs calculs, on va utiliser l’événement contraire :

$p(X\geqslant1)=1-p(\overline{X\geqslant1})$.

On peut voir ici que : 

$p(\overline{X\geqslant1})=p(X=0)$.

En effet, le contraire d’obtenir au moins une fois le chiffre 1 est de ne pas l’obtenir du tout.

On applique la formule du cours pour calculer $p(X=0)$ car $X$ suit la loi binomiale $\mathcal{B}\left(10, \dfrac{1}{6}\right)$.

On termine le calcul pour trouver $p(X\geqslant1)$. 

$p(X\geqslant1) \approx 0,838$ 

Espérance d’une variable aléatoire qui suit une loi binomiale

Si $X$ suit une loi binomiale de paramètres $n$ et $p$, alors :

$E(X)=n \times p$.

Exemple

Si $X$ suit la loi binomiale $\mathcal{B}\left(10, \dfrac{1}{6}\right)$, alors son espérance vaut :

$E(X)=10 \times \dfrac{1}{6}$

$E(X)=\dfrac{5}{3}$

Espérance de la loi binomiale

A savoir par coeur :

Si \(X\) suit une loi binomiale de paramètres \(n\) et \(p\), alors :

\(E(X) = n \times p\).

Les combinaisons

A savoir par coeur :

Une combinaison de \(p\) éléments de \(E\) est une partie de \(E\) qui contient \(p\) éléments.

Le nombre total de combinaisons à \(p\) éléments choisis parmi les \(n\) éléments de \(E\) est noté \((_{p}^n)\) et vaut :
\((_{p}^n) = \frac{n!}{p! \times (n – p)!} \).

Indépendance

Evénements indépendants 

Définition

Deux événements $A$ et $B$ sont indépendants lorsque : 

$p(A\cap B)=p(A)\times p(B)$

Ou encore de façon équivalente lorsque :

$\mathrm{p}_B(A)=p(A)$     ou    $\mathrm{p}_A(B)= p(B)$