Ensembles D et Q - Irrationnel
Ensemble $\mathbb{D}$ et $\mathbb{Q}$ – Irrationnel
On s’intéresse à des ensembles permettant de classifier les nombres.
Ensemble $\mathbb{D}$
Cela correspond à l’ensemble des décimaux.
Un nombre décimal est un nombre dont la partie décimale se termine, cela correspond donc à un nombre pouvant s’écrire sous la forme $\dfrac{a}{10^p}$ avec $a$ un entier et $p$ un entier.
Exemples :
$0,2 = \dfrac{2}{10^1}$, ainsi $a = 2$ et $p = 1$.
$-4,21 = \dfrac{-421}{100} = \dfrac{-421}{10^2}$. En effet, diviser par $100$ revient à décaler la virgule de deux rangs vers la gauche.
Ainsi $a = -421$ et $p =2$.
Ensemble $\mathbb{Q}$
Cet ensemble correspond à l’ensemble des rationnels, c’est à dire de l’ensemble des fractions, s’écrivant sous la forme $\dfrac{a}{b}$ avec $a$ et $b$ des entiers, et $b$ non nul.
Certaines fractions sont des nombres rationnels mais ne sont pas des nombres décimaux, c’est à dire qu’ils ne peuvent pas s’écrire sous la forme $\dfrac{a}{10^p}$ .
Exemples :
$\dfrac{2}{7} \in \mathbb{Q}$ mais $\dfrac{2}{7} \notin \mathbb{D}$ car la division de $2$ par $7$ ne se termine pas.
$\dfrac{-3}{4} \in \mathbb{Q}$ et $-\dfrac{3}{4} = – 0,75 = – \dfrac{75}{100} = – \dfrac{75}{10^2} \in \mathbb{D}$ .
Toutes les fractions sont donc rationnelles mais pas forcément décimales, mais toutes les fractions décimales sont rationnelles.
On note donc $\mathbb{D} \subset \mathbb{Q}$.
On peut aussi encadrer certaines nombres rationnels par des nombres décimaux.
Exemple :
On sait que $\dfrac{1}{3} \approx 0,3333…$
Ainsi, $0,33 \leq \dfrac{1}{3} \leq 0,34$ donne un encadrement à $10^{-2}$ près par des nombres décimaux de la fraction $\dfrac{1}{3}$.
Nombres irrationnels
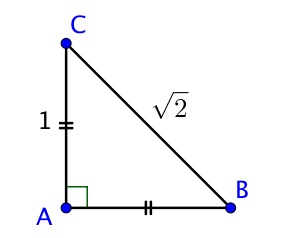
Soit $ABC$ un triangle isocèle rectangle en $A$,
D’après le théorème de Pythagore, on trouve que $BC^2 = AC^2 + AB^2 = 1 +1 = 2$ c’est à dire $BC = \sqrt{2}$.
Or ce nombre ne peut s’écrire sous aucune fraction et admet une partie décimale qui ne se termine pas : c’est un nombre irrationnel.
Ainsi, on sait que le segment $[BC]$ mesure $\sqrt{2}$ mais on ne connait pas la valeur exacte de ce dernier.
$\pi$ est aussi un nombre irrationnel.
En conclusion
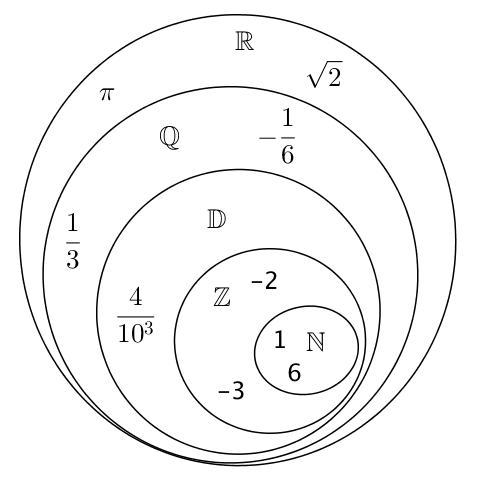
On peut représenter sous la forme d’un schéma la totalité des ensembles de nombres.
Ainsi, on connait l’ensemble des entiers naturels $\mathbb{N}$, l’ensemble des entiers relatifs l’ensemble des décimaux $\mathbb{D}$, l’ensemble des rationnels $\mathbb{Q}$ et enfin l’ensemble des réels $\mathbb{R}$ contenant l’ensemble des nombres précédents et les nombres irrationnels.