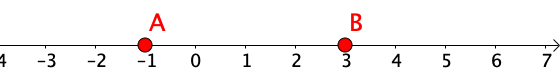Nombres relatifs, ordre

Les nombres relatifs, ordre

Les nombres relatifs – ordre

I) Définition

Les nombres relatifs sont constitués de nombres positifs et négatifs. 

II) Repérage sur une droite graduée

Une droite graduée se compose d’une origine, repérée par $0$, d’une longueur unité et d’un sens. 

On peut repérer un point grâce à son abscisse qui est un nombre relatif. 

Exemple :

Sur la droite graduée, on peut voir que l’abscisse du point $A$ est $-1$, on note alors $A(-1)$.

De même, on voit que l’abscisse du point $B$ est $3$.

On note donc $B(3)$. 

Définition

La distance à zéro d’un point correspond à la distance entre l’origine et ce point.

Exemple :

La distance à zéro du point $A$ est égale à la longueur du segment $[OA]$.

Ainsi comme $OA = 1$, la distance à zéro vaut $1$.

De même, la distance à zéro du point $B$ est égale à $OB$ et vaut donc $3$. 

III) Ordonner des nombres relatifs

Ordonner des nombres relatifs revient à classer ces nombres du plus petit au plus grand, par ordre croissant, ou du plus grand ou plus petit, par ordre décroissant. 

1) Comparer deux nombres de signes contraires 

Si on compare deux nombres de signes contraires, le plus grand est toujours le nombre positif. 

Exemple :

On souhaite comparer les nombres $-4,5$ et $3,2$.

Or $3,2 > 0$ et $-4,5 <0$.

De ce fait, on peut conclure que

$-4,5 < 3,2$. 

2) Comparer deux nombres négatifs 

Pour comparer deux nombres négatifs, il s’agit de comparer leur distance à zéro.

Le plus grand est le nombre qui a la distance à zéro la plus petite. 

Exemple :

On souhaite comparer les nombres $-3,5$ et $-6$.

La distance à zéro de $-3,5$ est $3,5$ et la distance à zéro de $-6$ est $6$.

Or, comme $3,5 < 6$ on a donc

$-3,5 > -6$. 

Bon à savoir :

Les nombres relatifs sont présents au quotidien.

On peut par exemple les retrouver :

• lorsque l’on parle de température. Lors de l’hiver, la température peut devenir négative et valoir $-10°$C par exemple qui est un nombre relatif
• dans les étages d’un immeuble, lorsque l’on se rend dans la cave à l’étage $-1$ qui est un nombre relatif.