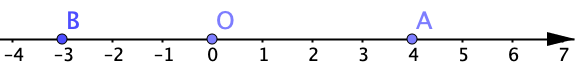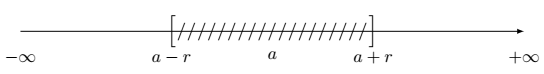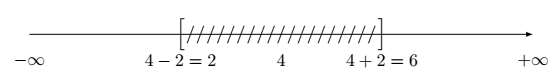Valeur absolue : distance entre deux nombres
La valeur absolue – Distance entre deux nombres
Définition : Valeur absolue
La valeur absolue d’un nombre $x$ se note $|x|$ et rend ce nombre positif.
Ainsi, si le nombre est positif, la valeur absolue du nombre est lui même.
Si le nombre est négatif, la valeur absolue est l’opposé de ce nombre.
On notera alors $\left \{ \begin{array}{l} |x| = x \text{ si } x \geq 0 \\ |x| = – x \text{ si } x \leq 0 \\ \end{array} \right.$
Exemples :
$|3| = 3$ car $3>0$
$|-2| = -(-2) = + 2$ car $-2 < 0$
$|\pi – 4 | = -(\pi – 4) = 4 – \pi$ car $\pi – 4 < 0$ en utilisant la calculatrice.
Distances
La distance entre deux nombres est toujours positive, on utilise donc la valeur absolue pour s’assurer de la positivité de nos calculs.
Exemples
On peut calculer des distances à l’origine.
Cette distance correspond à la valeur absolue de l’abscisse du nombre.
Ainsi, $|OA| = |4| = 4$ et $|OB| = |-3| = 3$.
Inégalités et valeurs absolues
On considère une inégalité de la forme $|x| \leq a$.
Cela signifie que la distance à l’origine doit être plus petite que $a$.
Cela correspond donc aux nombres $-a \leq x \leq a$.
Exemple
On représente sur la droite graduée l’ensemble des nombres $x$ tels que $|x| \leq 2$. On note cet ensemble sous la forme $-2 \leq x \leq 2$.
On considère à présent une inégalité de la forme $|x| > a$.
Cela correspond à l’ensemble des nombres dont la distance à l’origine est strictement plus grande que $a$. C’est à dire $x > a$ ou $x < -a$.
Exemple
$|x| > 2$ signifie $x < -2$ ou $x > 2$.
Distance entre deux nombres
La distance entre deux points $A$ et $B$ est donnée par la formule $AB = |x_A – x_B | = |x_B – x_A|$.
On notera que le résultat est toujours positif du fait de la valeur absolue.
Exemple
On considère les points $A$ et $B$ placés sur la droite graduée suivante.
Alors $AB = |x_A – x_B | = |x_B – x_A|$
$AB = |4 – (-3)| = |7| = 7$ ou bien $AB = |-3 – 4| = |-7| = 7$.
Dans les deux cas, la distance est bien positive et vaut $7$.
Inégalité $|x – a| \leq r$
Soit $a$ un nombre réel quelconque et $r$ un nombre positif.
On veut résoudre l’inégalité suivante $|x – a| \leq r$.
L’utilisation des valeurs absolues signifie qu’il s’agit d’une distance.
On commence alors par placer le point $a$ sur la droite graduée puis on cherche l’ensemble des nombres $M(x)$ d’abscisses $x$ tels que leur distance à $a$ soit inférieure ou égale à $r$.
On peut également traduire cette inégalité sous la forme
$-r \leq x – a \leq r$ ou en ajoutant $a$, on trouve l’inégalité suivante :
$-r + a \leq x \leq r + a$.
Ainsi, $x$ appartient à l’intervalle $[a -r; a + r]$.
Exemple
On cherche l’ensemble des points $M(x)$ d’abscisses $x$ tels que $|x – 4| \leq 2$.
On place donc le point $4$ sur la droite graduée puis on cherche l’ensemble des points dont la distance à $4$ est inférieure ou égale à $2$.
On trouve alors que $4-2 \leq x \leq 4 + 2$ ou encore $2 \leq x \leq 6$.