Racines n-ièmes de l’unité

Racines n-ièmes de l'unité

Les Racines n-ièmes de l’unité

Définition :

Soit $ n\in\mathbb{N^*}$, on appelle racine n-ième de l’unité tout nombre complexe $z$ qui vérifie $z^n=1$.

Intéressons-nous à la recherche des racines n-ièmes de l’unité .

On utilise l’écriture exponentielle d’un nombre complexe :

$\exists !\rho \in\mathbb{R^*}\;\;\exists ! \theta \in [0 ; 2\pi[\;\; z=\rho e^{i\theta}$

Soit $ n\in\mathbb{N^*}$, on résout $z^n=1$ :

$\Leftrightarrow\rho^n e^{ni\theta}=1$

$\Leftrightarrow \left\{\begin{array}{ll}\rho^n=1 \\n\theta=0+2k\pi\end{array}\right.$

$\Leftrightarrow \left\{\begin{array}{ll}\rho=1 \quad rq:\; \mathbb{U_n}\subset\mathbb{U}\ \\\theta=\frac{2k\pi}{n}\quad k\in\mathbb{Z }\end{array}\right.$

Donc l’ensemble des racines n-ièmes de l’unité :

$\mathbb{U_n}=\{1,\; e^{\frac{2I\pi}{n}} \; e^{\frac{4I\pi}{n}} \; ,…, \; e^{\frac{2(n-1)I\pi}{n}}\}$

$\mathbb{U_n}=\{\omega_k, 0\leq k \leq n-1\}\; , \; \omega _k=e^{\frac{2ik\pi}{n}}= \omega _1^k$

Il y a donc n racines n-ièmes de l’unité ($card(\mathbb{U_n})=n$).

On remarque que la somme des racines n-ièmes de l’unité est nulle :

$n\geq 2\quad\displaystyle\sum_{k=0}^{n-1} \omega _k=\displaystyle\sum_{k=0}^{n-1} \omega _1^k=\frac{1- \omega _1^n}{1- \omega _1}$

De plus :

$\overline{ \omega _k}^n=\overline{ \omega _k^n}=1 $

Donc $\overline{ \omega _k} \in\mathbb{U_n}$

Et $\overline{ \omega _k}=\overline{ e^{\frac{2ik\pi}{n}}}= e^{\frac{-2ik\pi}{n}}= e^{\frac{2i(n-k)\pi}{n}}$

Le conjugué d’une racine n-ième de l’unité est aussi une racine n-ième de l’unité.

Quelques cas particuliers :

• $n=2\quad \mathbb{U_2}=\{1;-1\}$
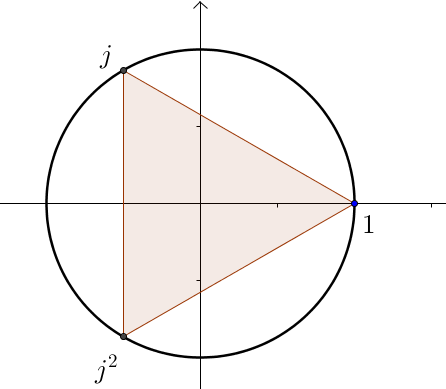
• $n=3\quad \mathbb{U_3}=\{1; e^{\frac{2i\pi}{3}}; e^{\frac{4i\pi}{3}}\}=\{1 ; j ; j^2 \}$

Avec $j= e^{\frac{2i\pi}{3}}$ et $j^2=\overline j $

Intéressons nous à l’image dans le plan complexe des racines 3-ièmes de l’unité.

$j$ correspond à $-\frac{1}{2}+i\frac{\sqrt 3}{2}$ et son conjugué $\overline j$ est son symétrique par rapport à l’axe des abscisses.

On a $1+j+j^2=0$ et l’image des trois racines cubiques dans le plan complexe forment un triangle équilatéral.

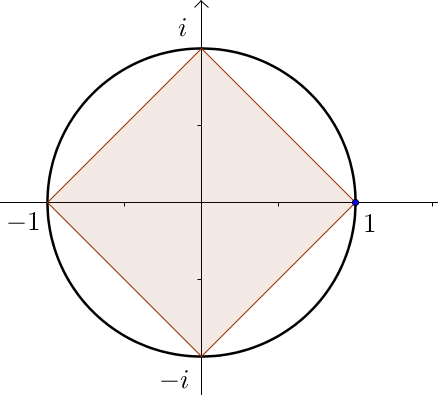
$n=4\quad \mathbb{U_4}=\{1;i ;-1 ;i \}$

Les 4 points sont sur le cercle trigonométrique et forment le sommet d’un polygone régulier.