Propriétés du son
I. Production
Le son est une sensation auditive. Pour créer un son, il faut mettre un objet en vibration, par exemple, une corde que l’on va pincer, ou alors la membrane d’un haut-parleur qui va vibrer.
II. Propagation
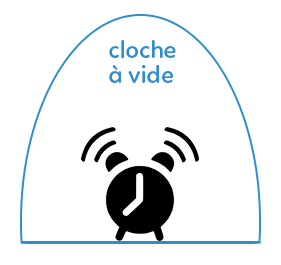
Le son va ensuite se propager mais pas dans n’importe quel matériau et, en particulier, il ne se propage pas dans le vide. C’est ce que l’on peut vérifier à travers l’expérience représentée ci-dessous.
Un réveil sonne dans une cloche à vide. On fait le vide donc on retire l’air. Le réveil continue à bouger, il vibre, il émet un son mais on ne l’entend pas. Le son ne se propage pas dans le vide !
III. Fréquence
Il existe des sons aigus et des sons graves. Ce qui fait la différence entre ces deux sons, c’est la fréquence qui caractérise un son. La fréquence se note f, elle s’exprime en hertz noté Hz. Plus la fréquence d’un son augmente et plus le son est aigu. Plus la fréquence d’un son diminue et plus le son est grave.
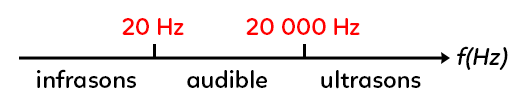
– Quand la fréquence augmente, il existe une fréquence à partir de laquelle on n’entend plus le son. La fréquence limite est d’environ 20 000 Hz. Au-dessus de 20 000 Hz, c’est le domaine des ultrasons.
– Quand la fréquence diminue, il existe une fréquence en dessous de laquelle on n’entend plus le son. La fréquence à partir de laquelle on ne l’entend plus est d’environ 20 Hz. C’est le domaine des infrasons.
– Entre les infrasons et les ultrasons c’est le domaine audible. 20 Hz et 20 000 Hz sont des fréquences moyennes, cela dépend de l’âge, des oreilles, etc.
IV. Niveau sonore
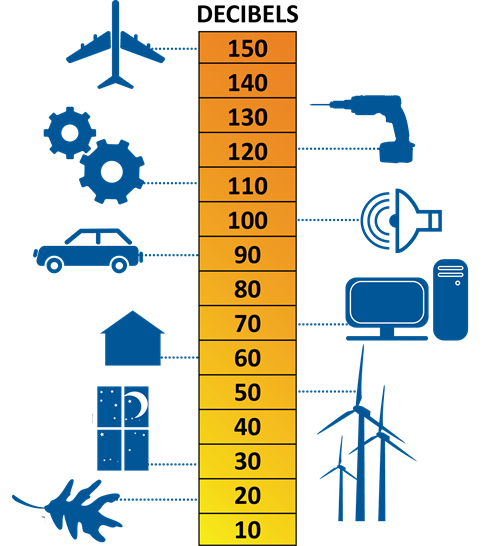
Le niveau sonore caractérise le son. Plus un son est intense, plus le niveau sonore est important. Le niveau sonore s’exprime en décibels (dB). Il existe des échelles en décibels qui mesurent les différents niveaux sonores existants.
Un son qui a un niveau sonore très élevé et que l’on écoute pendant une durée importante, représente un vrai danger pour l’oreille.
Année-lumière
Année-lumière
L’année-lumière est la définition d’une unité de distance. Pour bien comprendre ce qu’est une année-lumière, on s’interroge sur la propagation de la lumière. La lumière se propage dans certains matériaux et se propage aussi dans le vide. On étudie ici, la vitesse de la lumière dans le vide.
I. Vitesse de la lumière dans le vide
La vitesse de la lumière dans le vide est la plus grande vitesse que l’on peut atteindre, on l’appelle souvent la célérité. On la note c et sa valeur est 300 000 km/s. Il ne faut pas connaître la valeur par cœur mais il faut savoir la reconnaître et savoir que lorsque l’on voit un c c’est la célérité.
II. Année-lumière : distance parcourue par la lumière en un an
L’année-lumière est la distance parcourue par la lumière en un an. Pour calculer cette distance, on peut utiliser la relation $vitesse = \dfrac{distance}{durée}$.
(Durée en secondes : 1 an = 365 jours ; 1 jour = 24 h ; 1 h = 60 min ; 1 min = 60 s.)
C’est la distance qui nous intéresse donc on a :
$distance = vitesse \times durée = 300 \ 000 \times 365 \times 24 \times 60\times 60 = 9 \ 500 \ 000 \ 000 \ 000 \ km = 9,5 \times 10^{12} \ km$.
C’est une très grande valeur qui est utilisée pour les distances astronomiques.
III. Conversions
On a toujours la relation $1a.l = 9,5.10^{12} km.$
Années-lumières en kilomètres
Par exemple, une galaxie est à 4,2 a.l.
On fait un produit en croix. $4,2 a.l = 4,2\times 9,5 \times 10^{12} = 40\times 10^{12} \ km$.
Kilomètres en années-lumières
Par exemple, une étoile se situe à $1,5.10^{14}\ km.$
$\dfrac{1,5\times 10^{14}}{9,5\times 10^{12}} = 16 \ a.l$.
Pour passer des a.l aux km, il faut multiplier par $9,5.10^{12}.$
Pour passer des km aux a.l, il faut diviser par $9,5.10^{12}.$
Mesure de distance avec le son et la lumière
Mesure de distance avec le son et la lumière
I. Principe
On utilise deux propriétés du son et de la lumière : la propagation en ligne droite et la réflexion sur certains objets. Le principe de cette méthode pour mesurer des distances est le suivant :
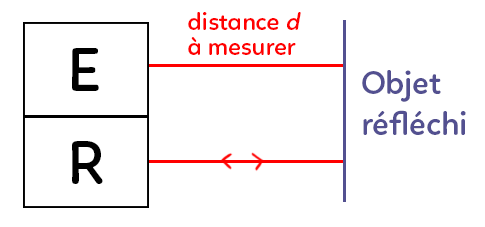
On place un émetteur et un récepteur au même endroit et un objet réflecteur situé à la distance que l’on doit mesurer. On envoie par l’émetteur un signal, qui peut être le son ou la lumière, qui va atteindre l’objet réflecteur puis ce signal va se réfléchir dans l’autre sens pour rejoindre le récepteur. On mesure alors la durée qu’il faut pour faire un aller-retour. Cette durée sera notée $∆t.$
Une fois la durée $∆t$ obtenue ainsi que la vitesse du son ou de la lumière dans le milieu, on peut déterminer la distance qui sépare l’émetteur et le récepteur de l’objet réflecteur.
Pour cela, on utilise la formule $vitesse = \dfrac{distance}{durée}$.
Dans notre cas : $v = \dfrac{2d}{∆t}$.
II. Distance Terre-Lune
Pour mesurer la distance Terre-Lune, les Hommes qui ont été sur la Lune ont mis un réflecteur dessus. On envoie depuis la Terre un signal laser qui part sur la Lune, se réfléchit puis revient sur la Terre.
La durée qu’il faut pour que ce faisceau laser fasse l’aller-retour est de 2,43 s.
Sachant que c = 300 000 km/s, pour calculer la distance on a :
$v = \dfrac{2d}{∆t}$ donc $2d = v\times ∆t$ alors $d = \dfrac{v\times ∆t}{2}$.
Donc : $d = \dfrac{300 000\times 2,43}{2} = 364 500 \ km$.
III. Sonar
Dans le cas du sonar, on utilise le son et même des ultrasons. Le bateau émet des ultrasons qui vont toucher les fonds marins dont on souhaite savoir la profondeur, puis les ultrasons se réfléchissent sur les fonds marins et reviennent sur le bateau.
Dans notre exemple, il faut 1,3 s pour faire l’aller-retour et donc pour déterminer la distance qui sépare le bateau et les fonds marins, on fait le même calcul mais cette fois-ci avec la vitesse des ultrasons :
$v = 1500 \ m/s$
$d = \dfrac{1500\times 1,3}{2} = 975 \ m$.