Inégalités - Opérations
Inégalités – Opérations
Rappels :
1) Fonction croissante :
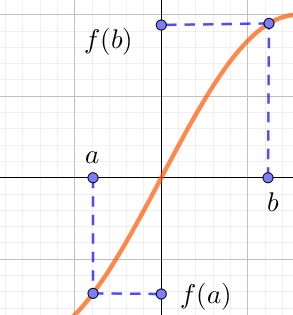
Une fonction $f$ est croissante sur un intervalle $I$ si pour tous réels $a$ et $b$ appartenant à $I$ tels que $a < b$, alors $f(a) < f(b)$.
Exemple :
Soit $f$ la fonction linéaire définie par $f(x) = \lambda x$ avec $\lambda > 0$ et $x \in \mathbb{R}$.
Alors $f$ est croissante.
2) Fonction décroissante :
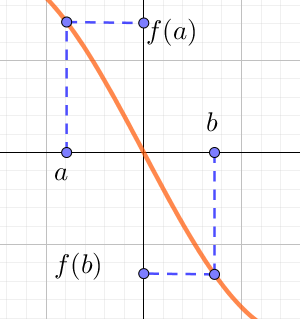
Une fonction $f$ est décroissante sur un intervalle $I$ si pour tous réels $a$ et $b$ appartenant à $I$ tels que $a < b$, alors $f(a) > f(b)$.
Exemple :
Soit $f$ la fonction linéaire définie par $f(x) = \lambda x$ avec $\lambda < 0$ et $x \in \mathbb{R}$.
Alors $f$ est décroissante.
Sommes avec des inégalités
Soient $a, b, c$ et $d$ des réels,
Si $a < b$ et $c < d$ alors $a + c < b + d$ en additionnant terme à terme
Il faut cependant faire prêter une attention particulière à certains points.
En effet, si $a < b$ et $c \leq d$, la propriété de somme est toujours vraie mais il faut garder le signe d’inégalité stricte.
Ainsi, $a + c < b + d$.
De plus, si les inégalités ne sont pas écrites dans le même sens il faut les réécrire pour que les signes d’inégalité soient les mêmes.
Ainsi, si $a \leq b$ et $c \geq d$, on écrira $d \leq c$ et on appliquera la propriété pour additionner les deux inégalités : $a + d \leq b + c$.
Produit par un réel $\lambda$
Soient deux réels $a$ et $b$,
a) On suppose tout d’abord que $\lambda >0$,
Si $a > b$, en multipliant à gauche et à droite par $\lambda$ on trouve $\lambda a > \lambda b$.
Le sens de l’inégalité n’a pas changé.
Cela revient à appliquer la fonction $f(x) = \lambda x$ qui est croissante car $\lambda >0$.
Exemple :
On a $4 > 1$, en multipliant par $3$ on obtient $12 > 3$ ce qui est vraie.
b) On suppose ensuite que $\lambda < 0$,
Si $a > b$, en multipliant à gauche et à droite par $\lambda$ on trouve $\lambda a < \lambda b$.
Le sens de l’inégalité est inversé.
Cela revient à appliquer la fonction $f(x) = \lambda x$ qui est décroissante car $\lambda < 0$.
Exemple :
On a $4 > 1$, en multipliant par $-2$ on obtient $-8 < -2$ : on a changé le sens de l’inégalité.