Suites numériques, variations
Suites numériques, variations
Les différentes façons de définir une suite
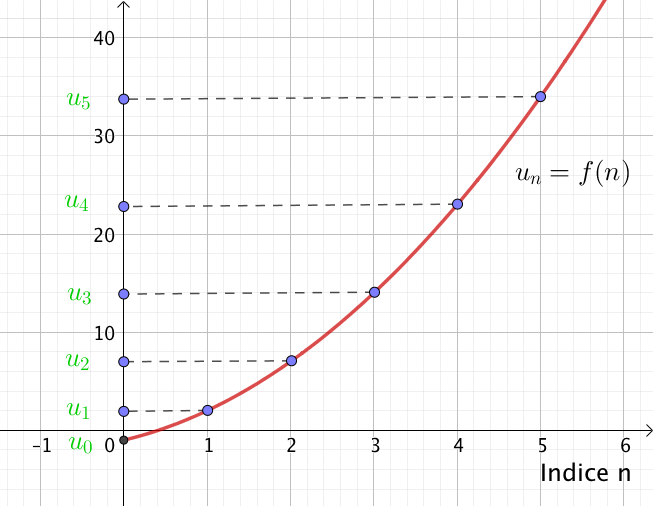
La première définition est la définition explicite, c’est à dire que $u_n$, le terme de rang $n$, est exprimé directement en fonction de $n$ comme par exemple $u_n = 3n + 2$, $u_n$ s’écrit donc sous la forme : $u_n = f(n)$.
Une autre manière de définir une suite est la définition par récurrence, c’est-à-dire que $u_{n + 1}$ est défini en fonction de $u_n$ comme :
$\left \{ \begin{array}{l} u_0 = 1 \\ u_{n + 1} = 2u_n – 5 \\ \end{array} \right.$
On a bien : $u_{n + 1} = f(u_n)$ (avec $f(x)=2x-5$).
Pour trouver un terme de la suite, il faut avoir d’abord calculé ceux qui le précèdent.
Enfin, il est possible de définir une suite de manière implicite dans des problèmes de géométrie ou d’économie par exemple.
Majorant, minorant
Si pour tout $n \in \mathbb{N}, \ u_n \leq M$ alors $M$ est un majorant de la suite.
Si pour tout $n \in \mathbb{N}, \ u_n \geq m$ alors $m$ est un minorant de la suite.
Si une suite est à la fois minorée et majorée (comprise entre $m$ et $M$), elle est bornée.
Les variations
Si pour tout $n \in \mathbb{N}, \ u_{n + 1} \geq u_n$ alors $(u_n)$ est croissante.
Si pour tout $n \in \mathbb{N}, \ u_{n + 1} \leq u_n$ alors $(u_n)$ est décroissante.
Représentation graphique d'une suite
Représentation graphique d’une suite
La représentation graphique d’une suite est un nuage de points dont l’abscisse correspond aux entiers naturels et permet d’émettre des conjectures sur le sens de variation de la suite ou sa convergence sans pour autant constituer une démonstration rigoureuse.
Il existe deux formes de suites, les suites explicites ($u_n = f(n)$) et les suites récurrentes ($u_{n + 1} = f(u_n)$).
Pour représenter une suite explicite, on peut calculer tous les termes de la suite puis les placer sur le graphique ou bien on représente la fonction par laquelle $(u_n)$ est définie pour tout réel positif puis on place sur la courbe de la fonction les points d’abscisse entière.
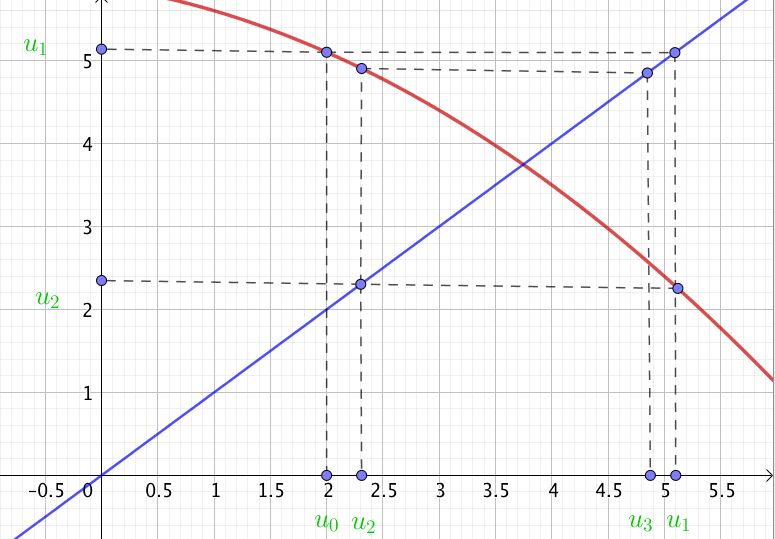
Afin de représenter une suite récurrente, on peut tout d’abord calculer les termes puis les placer sur le graphique. une autre méthode consiste en la construction de la suite. On commence par tracer la fonction $y = f(x)$. Or, $u_{n + 1}$ est l’image de $u_n$ par la fonction $f$. On commence donc par placer $u_0$ sur l’axe des abscisses puis on obtient $u_1$ comme étant l’image par la fonction $f$ de $u_0$. Afin de trouver $u_2$ comme image de $u_1$ par $f$, on reporte $u_1$ sur l’axe des abscisses grâce à la courbe d’équation $y = x$.
Puis on recommence le procédé : c’est une construction par escaliers. Cette construction est interessante pour constater l’évolution de la suite sans calculer ses termes. Enfin, pour représenter graphiquement cette suite, il faut tracer un nuage de points comme pour les formes explicites.