Suites tendant vers l'infini
Suites tendant vers l’infini
Définition :
Une suite de réels $(u_n)_{n \in \mathbb{N}}$ a pour limite $+ \infty$ lorsque $n$ tend vers $+ \infty$ si et seulement si tout intervalle de la forme $[A; +\infty [$, avec $A \in \mathbb{R}^*_+$, contient tous les termes à partir d’un certain rang.
On note alors : $\lim \limits _{n \to + \infty} u_n = + \infty$
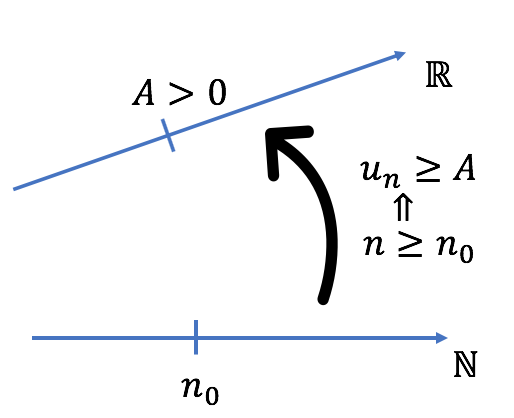
On trace la droite des réels et la “droite” des entiers naturels. On place sur la droite des réels un réel $A$ positif. Quelque soit le réel $A$ choisit, il existe un entier naturel $n_0$, dépendant de $A$, tel que pour tout $n \geq n_0$, $u_n \geq A$.
Cela signifie que l’intervalle de la forme $[A; +\infty [$ contient la quasi totalité des termes de la suite. En effet, il existe un nombre fini de termes de la suite n’appartenant pas à l’intervalle $[A; +\infty [$ : il y en a exactement $n_0$.
Mathématiquement, cela se traduit par l’énoncé suivant :
$\forall A > 0, \exists n_0 \in \mathbb{N} | \forall n \in \mathbb{N}, n \geq n_0 \Rightarrow u_n \geq A$
Ou encore :
Pour tout $A > 0$ il existe $n_0 \in \mathbb{N}$, dépendant de $A$, tel que pour tout $n \in \mathbb{N}$, on a $n \geq n_0 \Rightarrow u_n \geq A$.
Exemple :
Soit $n \in \mathbb{N}$,on pose $u_n = n^2 + 2,n +5$.
On cherche à démontrer qu’il existe au moins un $n_0$ pour $A$ fixé quelconque.
Soit $A > 0$, on cherche un $n_0$ qui convient.
On souhaite avoir $n^2 + 2n + 5 \geq A$.
On raisonne par condition suffisante.
Comme $n^2 + 2n + 5 \geq n^2$, pour avoir $n^2 + 2n + 5 \geq A$ il suffit d’avoir $n^2 \geq A$ c’est à dire $ n \geq \sqrt{A}$ (par croissance de la fonction racine carrée).
Cependant $\sqrt{A}$ n’est généralement pas un entier naturel, on ne peut donc pas dire que $n_0 = \sqrt{A}$.
On choisit alors $n_0 = \lfloor A \rfloor + 1$, avec $\lfloor A \rfloor$ la partie entière de $\sqrt{A}$ qui est égale au plus grand entier plus petit que $\sqrt{A}$.
Dans ce cas, si $n \geq n_0$ alors $n \geq \sqrt{A}$ d’où $n^2 \geq A$
Donc $n^2 + 2n + 5 \geq n^2 \geq A$, c’est à dire $u_n \geq A$.
Ainsi, $\lim \limits _{n \to + \infty} u_n = + \infty$.
Définition :
Une suite de réels $(u_n)_{n \in \mathbb{N}}$ a pour limite $- \infty$ lorsque $n$ tend vers $+ \infty$ si et seulement si tout intervalle de la forme $]-\infty; B [$, avec $B \in \mathbb{R}^*_-$, contient tous les termes à partir d’un certain rang. On note alors : $\lim \limits _{n \to + \infty} u_n = – \infty$
Mathématiquement, cela se traduit par l’énoncé suivant :
$\forall B < 0, \exists n_0 \in \mathbb{N} | \forall n \in \mathbb{N}, n \geq n_0 \Rightarrow u_n \leq B$
Ou encore :
Pour tout $B < 0$ il existe $n_0 \in \mathbb{N}$, dépendant de $B$, tel que pour tout $n \in \mathbb{N}$, on a $n \geq n_0 \Rightarrow u_n \leq B$.
Remarque :
$(u_n)$ tend vers $- \infty$ si et seulement si $(-u_n)$ tend vers $+ \infty$.
Démonstration :
On commence par démontrer que si $(-u_n)$ tend vers $+ \infty$, alors $(u_n)$ tend vers $- \infty$.
Soit $B < 0$,
On pose $A = – B > 0$, comme $(-u_n)$ tend vers vers $+ \infty$, alors il existe $n_0 \in \mathbb{N}$ tel que $n \geq n_0 \Rightarrow -u_n \geq A$.
Donc pour $n \geq n_0$, on a $-u_n \geq – B$ d’où pour $n \geq n_0$, on a $u_n \leq B$.
On démontre ensuite que si $(u_n)$ tend vers $- \infty$, alors $-(u_n)$ tend vers $+ \infty$.
Soit $A > 0$,
On pose $B = – A < 0$, comme $(u_n)$ tend vers vers $- \infty$, alors il existe $n_0 \in \mathbb{N}$ tel que $n \geq n_0 \Rightarrow u_n \leq B$.
Donc pour $n \geq n_0$, on a $u_n \leq -A$ d’où pour $n \geq n_0$, on a $-u_n \geq A$.
Exemple :
On sait que $\lim \limits _{n \to + \infty} n^2 = + \infty$, ainsi, $\lim \limits _{n \to + \infty} (-n^2) = – \infty$.
Remarque :
Si $f$ est une fonction telle que $\lim \limits _{+ \infty} f = + \infty$, alors la suite de terme général $f(n)$ tend vers $+ \infty$