Construction de symétriques
Symétrie axiale
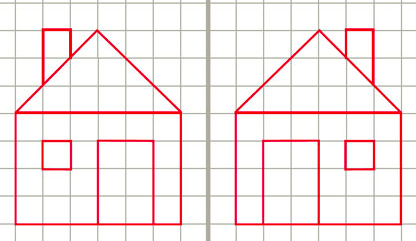
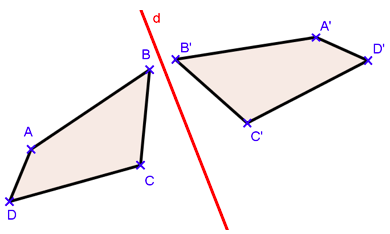
Définition : figures symétriques
Deux figures symétriques par rapport à un axe (d) sont deux figures qui se superposent si on plie la feuille suivant la droite (d).
Définition : points symétriques
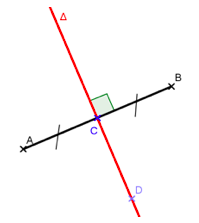
Deux points $A$ et $B$ sont symétriques par rapport à une droite $\Delta$ signifie que $\Delta$ est la médiatrice du segment $[AB]$.
C’est-à-dire : $\Delta$ est perpendicumaire à $(AB)$ et passe par le milieu de $[AB]$ (ici le point $C$)
Attention : un point de l’axe est son propre symétrique ! Ici $D$ est son propre symétrique par rapport à $\Delta$.
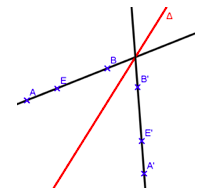
Pour construire le symétrique d’une figure géométrique, on construit le symétrique de chaque sommet de cette figure grâce à la définition puis on utilise les propriétés suivantes :
Propriétés :
1) Le symétrique d’une droite est une droite.
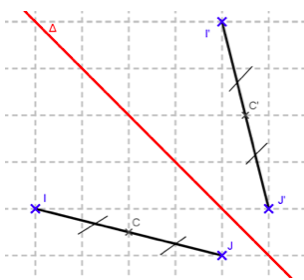
2) Le symétrique d’un segment est un segment de même longueur.
3) Le symétrique d’un polygone est un polygone semblable.
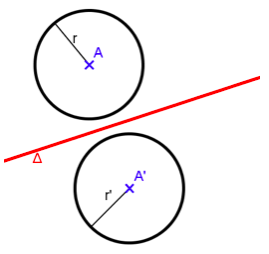
4) Le symétrique d’un cercle est un cercle de même rayon.
Remarque :
On rencontre cette symétrie assez souvent, lorsqu’on regarde dans un miroir ou qu’on observe le reflet d’un paysage dans une rivière ou un lac…
Axes de symétrie
AXES DE SYMETRIE
Définition
Une droite est un axe de symétrie d’une figure lorsque cette figure est son propre symétrique par rapport à cet axe.
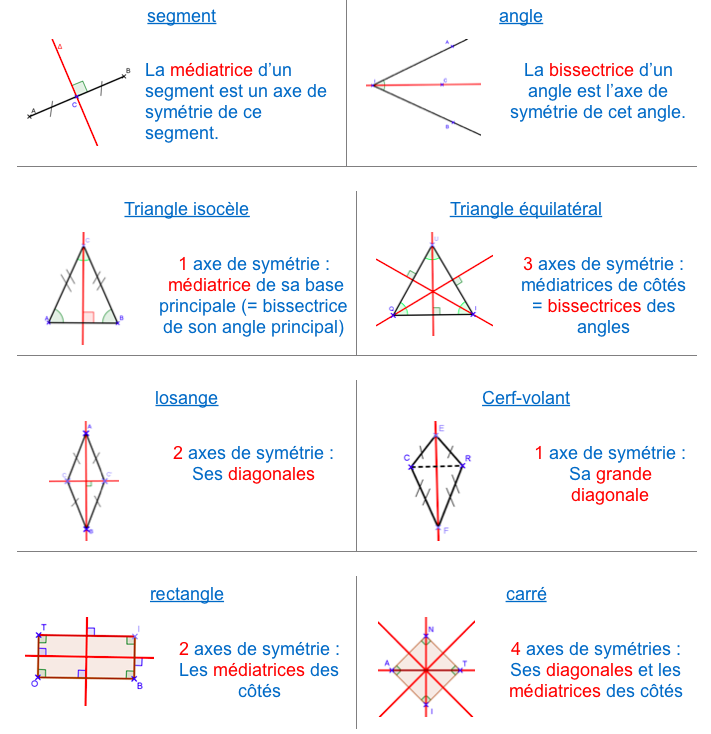
Les axes de symétrie des figures usuelles