Taux global & taux réciproque
Taux global & taux réciproque
Taux global, évolutions successives
Un nombre $V_0$ peut évoluer, il peut subir des augmentations ou des diminutions successives jusqu’à une valeur finale $V_n$ que l’on souhaite déterminer.
Pour ce faire, il s’agit de multiplier la valeur initiale par le coefficient multiplicateur global, défini par :
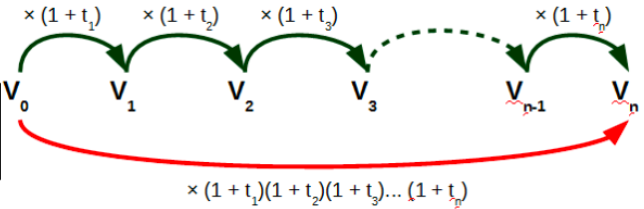
$ 1 +t_g = (1 + t_1) \times (1 + t_2) \times (1+t_3) \times …\times (1+t_n)$
où $( 1 + t_1)$ est le coefficient multiplicateur de la première évolution, $(1 + t_2)$ le coefficient multiplicateur de la seconde évolution, etc.
Ainsi pour obtenir le coefficient multiplicateur global, il faut multiplier les coefficients multiplicateurs des évolutions entre-eux.
Par exemple, un salaire de 2547,5 € baisse de 3% puis augmente de 12%, il en résulte alors qu’il vaut
$S = 2547,5 \times \left ( 1 – \dfrac{3}{100} \right ) \times \left ( 1 + \dfrac{12}{100} \right ) $
$S= 2547,5 \times 0,97 \times 1,12 = 2767,6$ €.
On remarquera qu’il ne faut pas additionner les pourcentages des évolutions pour trouver le résultat final.
Taux réciproque
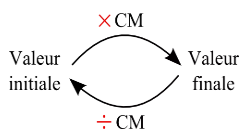
Si un nombre évolue d’une valeur initiale à une valeur finale avec un coefficient multiplicateur $CM= (1 + t)$, alors pour revenir à la valeur initiale, il faut multiplier la valeur finale par $\dfrac{1}{1 + t}$, (ce qui revient à diviser par $CM$)
En d’autres termes, le nouveau coefficient multiplicateur est défini par $ 1 + t’ = \dfrac{1}{1 + t}$.
Par exemple, une maison subit une hausse de 15%. Calculons le pourcentage de la baisse pour revenir au prix initial :
$1 + t’ = \dfrac{1}{1 + 0,15}$, c’est à dire $t’ = \dfrac{1}{1 + 0,15} – 1 \approx -0,1304$, soit une baisse de 13% environ.