Théorème des gendarmes
Le théorème des gendarmes
Théorème
Soient $I$ un intervalle de $\mathbb{R}$ et $a$ une borne de $I$ ($a$ est réel ou infini).
Si $f$, $g$, et $h$ sont trois fonctions définies sur $I$ telles que, pour tout $x\in I$ : $ f(x) \leqslant g(x) \leqslant h(x) $
Si de plus $\displaystyle \lim_{x\to a} f(x) = \lim_{x\to a} h(x) = \ell$ avec $\ell\in \mathbb{R}$, alors :
$\displaystyle \lim_{x\to a} g(x) = \ell$
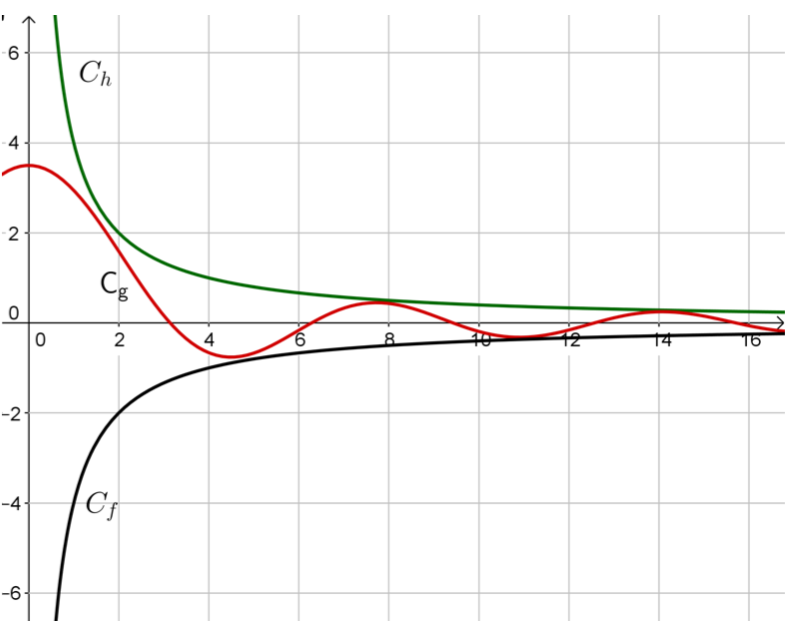
Illustration graphique
Le calcul d’une limite se fait très régulièrement par l’intermédiaire d’inégalités. Il est important d’avoir quelques inégalités en tête lors d’un exercice sur les fonctions.
En voici quelques-unes des plus utiles dans le cadre du théorème des gendarmes :
Pour tout $x\in\mathbb{R}$, $e^x\geqslant x+1$.
Pour tout $x\in \mathbb{R}$, $|\sin(x)|\leqslant 1$ et $|\cos(x)|\leqslant 1$.
Pour tout $x>0$, $\ln(x)\leqslant x-1$.
Théorème des gendarmes - Exercice 1
Exercice
Soit\(f(x) = \dfrac{1}{x + cos x}\) une fonction définie sur
\(D_f = [\pi ; +\infty[\).
Étudions \( \displaystyle\lim_{x\to +\infty} f(x)\).
Ce qu’il faut savoir faire :
- Étape 1 : On sait que pour tout \(x\) appartenant a \(Df\), \(\cos(x)\) est compris entre \(-1\) et \(1\).
- Étape 2 : On poursuit l’encadrement pour retrouver la fonction \(f\).
- Étape 3 : On calcule la limite en l’infini des $2$ fonctions encadrant \(f\).
- Étape 4 : On peut conclure grâce au théorème des gendarmes que la limite en l’infini de \(f\) est \(0\).