Transfert thermique : conduction
I. La conduction
C’est un transfert thermique donc un échange d’énergie. Il y a deux caractéristiques : par contact et sans déplacement de matière.
Exemple 1 : une barre de fer que l’on chauffe à une de ses extrémités, par conduction, le reste de la barre de fer se réchauffe aussi. Effectivement, il n’y a pas de déplacement de matière, la barre de fer ne se disloque pas, elle est solide. Et, c’est bien par contact car les différentes particules qui composent la barre de fer sont bien en contact les unes avec les autres.
Exemple 2 : c’est l’échange qu’il peut y avoir entre l’intérieur et l’extérieur d’une maison. De ce fait, le transfert d’énergie entre l’intérieur et l’extérieur de la maison, au niveau des murs, il n’a pas lieu par déplacement de matière : les murs ne bougent pas. Donc, comme il n’y a pas de déplacement de matière, on entre dans la catégorie de la conduction. Puisqu’il y a échange d’énergie, cela veut dire que chaque seconde, il y a de l’énergie qui passe à travers la paroi.
II. Calcul du flux thermique Φ
Φ est le flux thermique exprimé en J/s donc en Watts. C’est la même unité qu’une puissance.

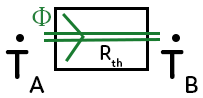
Voici un schéma de la situation. Il y a une paroi, caractérisée par sa résistance thermique $R_{th}.$ D’un côté, il y a une température $T_A$ de la paroi, de l’autre côté une température noté $T_B$. Sur ce schéma $T_A > T_B$, et il faut savoir, que les transferts thermiques se font toujours de la source chaude vers la source froide. Donc le flux thermique va du côté où $T_A > T_B$ (de gauche à droite).
Comment calculer ce flux thermique ? Il y a deux formules distinctes :
$\Phi = \dfrac{Q}{\Delta t}$
$Q$ est la quantité de chaleur transférée par la paroi pendant la durée $\Delta t$. Elle s’exprime en Joules (J). $\Delta t$ est la durée en secondes (s). Si on analyse cette formule en termes d’unité, on voit bien que l’unité de $\Phi$ est en J/s.
$\Phi = \dfrac{T_A-T_B}{R_{th}}$
On utilise souvent celle-ci car elle permet de calculer $\Phi$ en ne tenant compte que des températures avant et après la paroi et en tenant compte de la résistance thermique de cette paroi. $\Phi$ est toujours en J/s, $T_A-T_B$ est une différence de température, soit en °C soit en K. Ce qui compte ce n’est pas la valeur de la température mais la différence donc peu importe l’unité. La résistance thermique est en K.W-1. Soit l’exercice donne la résistance thermique, soit il y a une autre formule pour calculer la résistance thermique d’une paroi.
$ R_{th} = \dfrac{e}{\lambda S}$
La résistance thermique est proportionnelle à l’épaisseur $e$ de la paroi (m), et inversement proportionnelle à la conductivité thermique du matériau de la paroi $\lambda$ (en W.m-1.K-1) et à la surface d’échange $S$ (m2). Donc, plus la surface d’échange est grande, plus la résistance thermique est petite. De même pour la conductivité thermique. La conductivité thermique est en référence aux matériaux qui composent la paroi. Systématiquement dans un exercice, on donne la valeur de la conductivité selon la paroi : si on a un mur en béton, un mur en laine de verre, etc., on a une conductivité différente. Plus la conductivité thermique est grande, meilleure se fait la conduction thermique. Si on recherche un matériau isolant, il vaut mieux avoir une conductivité thermique la plus faible possible. Dans ce cas-là, le matériau est très isolant et résiste très fort au transfert thermique.
III. Analogie avec l’électricité
|
Schéma |
Source du tranfsert |
Formule |
|
|
$V_A \ne V_B$ |
$V_A – V_B = R \times i$ |
|
|
$T_A \ne T_B$ |
$T_A – T_B = R_{th}\times \Phi$ |
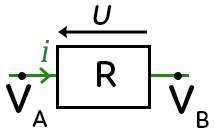
On prend le cas d’une résistance caractérisée par la valeur de la résistance $R,$ un fil électrique, le potentiel électrique est $V_A$ en amont et $V_B$ en aval. L’intensité qui passe à travers la résistance est notée $i$, et $U$ est la différence de potentiel. $U$ est égal à $V_A – V_B.$
Quand on fait le schéma d’une paroi, il y a quelque chose de similaire. La zone de la paroi est caractérisée par une résistance qu’on appelle résistance thermique $R_{th}.$ Les températures se transforment en potentiels. Il n’y a pas de courant électrique mais il y a quand même un flux énergétique $\Phi$ en J/s. Ensuite, les sources du transfert correspondent à $V_A \ne V_B$, comme les potentiels électriques sont différents il y a du courant qui circule.
Ici, c’est la différence de températures comme TA ≠ TB, il va y avoir un transfert thermique. Dans la formule, on repère aussi des équivalences : on sait que $V_A – V_B = R \times i$ donc on a $T_A – T_B = R_{th}\times \Phi.$
En faisant ces analogies en électricité, on peut retrouver les formules que l’on a vu sur la conduction.
Transfert thermique : convection et rayonnement
I. La convection
La convection est un échange énergétique (un transfert thermique) par le biais d’un échange de matière. Quand il y a un fluide avec une partie chaude et une partie froide, la partie chaude monte tandis que la partie chaude descend. Cela dépend de la densité du milieu :
– S’il est chaud et qu’il monte, c’est parce qu’il a une densité plus faible.
– S’il est froid et qu’il descend, c’est parce qu’il a une densité plus importante.
Exemple 1 : l’air réchauffé par un radiateur : comment se fait-il qu’une pièce se réchauffe grâce à un radiateur ? Grâce à la convection. L’air qui passe à côté du radiateur reçoit de l’énergie et par convection cet air se déplace dans les autres endroits de la pièce. En se déplaçant, il déplace lui-même l’air qu’il remplace et celui-ci passe à son tour devant le radiateur et se réchauffe, etc. C’est de cette façon que tout une pièce finie par être réchauffée.
Exemple 2 : l’eau dans une casserole. Si le bas, le milieu et la surface de l’eau est chaude c’est qu’il y a eu un mouvement convectif au sein de la casserole. C’est principalement les bords qui chauffent dans la casserole et surtout celui du bas. Donc, s’il y a bien une raison pour laquelle la température a réussi à s’équilibrer à l’intérieur de l’eau : c’est par convection.
II. Le rayonnement
Le rayonnement est un échange thermique par le biais des bandes électromagnétiques. Il existe différents types d’ondes : mécaniques, sonores, ondes électromagnétiques, etc. Parmi les ondes électromagnétiques, on trouve :
– les infrarouges (IR),
– la lumière visible,
– les ultra-violets (UV).
Les infrarouges sont ceux qui réchauffent. La lumière visible et les UV sont davantage énergétiques. Les UV nous font attraper des coups de soleil, ils nous brûlent la peau.
Les ondes électromagnétiques se propagent dans le vide, dans des milieux transparents, mais aussi dans le vide. Il n’y a pas besoin de milieu matériel alors que pour la conduction ou la convection, il y a besoin d’un milieu.
Exemple : le chauffage au gaz installé en terrasse, le feu de cheminée sur l’extérieur, le Soleil sur la Terre. L’air est un très mauvais conducteur thermique.
Deux lois à connaître :
La loi de Wien (rappel de 1re) : elle concerne les corps noirs. Ce qui correspond à la modélisation d’un corps chauds. On a $λ_{max}.T = 2,893.10^{-3}$, $λ_{max}$ est la longueur d’onde principalement émise (en m) et T la température en K. Leur produit donne une constante exprimée en m.K.
La loi de Stefan : c’est une autre loi qui concerne encore les corps noirs, qu’on aime utiliser pour représenter les émetteurs importants comme le Soleil. On a : $P = σ.S.T^{4}$, avec P la puissance totale rayonnée par un corps noir (en W), σ la constante de Stefan (σ = 5,67.10-8 W.m-2.K-4), S est la surface émettrice (en m2) et T la température (en K).