Les triangles particuliers
Triangles particuliers
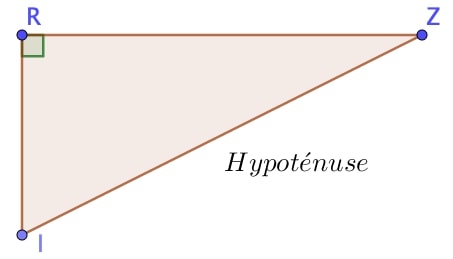
Triangle rectangle
Un triangle rectangle est un triangle qui a un angle droit.
$(RI)\perp (RZ)$ donc le triangle $RIZ$ est rectangle en $R$.
$[IZ]$, le côté opposé à l’angle droit, est le plus long côté de ce triangle et est appelé l’hypoténuse de ce triangle.
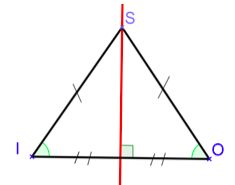
Triangle isocèle
Un triangle isocèle est un triangle qui a deux côtés de même longueur.
$IS=SO$ donc $ISO$ est un triangle isocèle en $S$.
$S$ est appelé son sommet principal et $[IO]$ sa base principale.
Ce triangle admet pour axe de symétrie la médiatrice de $[IO]$ qui est aussi la bissectrice de l’angle. Et par conséquent les deux angles à la base $\widehat{SIO}$ et $\widehat{SOI}$ ont la même mesure.
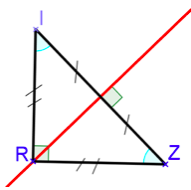
Triangle rectangle isocèle
Un triangle rectangle isocèle est un triangle qui est à la fois rectangle et isocèle, il a donc un angle droit et deux côtés de même longueur.
$IR=RZ$ et donc $RIZ$ est rectangle isocèle en $R$.
Un triangle rectangle isocèle a les propriétés du triangle rectangle et celles du triangle isocèle :
-Il a un axe de symétrie : la médiatrice de la base principale $[IZ]$ (ou de l’hypoténuse) qui est aussi la bissectrice de l’angle droit.
-Ses deux angles aigus $\widehat{RIZ}$ et $\widehat{RZI}$ ont la même mesure.
Triangle équilatéral
Un triangle équilatéral est un triangle dont les trois côtés ont la même longueur.
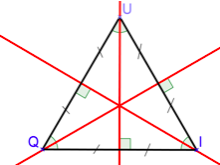
$QU=UI=QI$ donc $QUI$ est un triangle équilatéral.
-Un triangle équilatéral admet trois axes de symétrie : les médiatrices de chacun de ses côtés qui sont aussi les bissectrices de ses angles.
-Les trois angles d’un triangle équilatéral ont tous la même mesure. (60°)
Commentaire : Un triangle équilatéral est en fait un triangle qui est trois fois isocèle, il est isocèle en chacun de ses sommets.