Maximum, minimum d'une fonction
Maximum, minimum d’une fonction
Une situation concrète
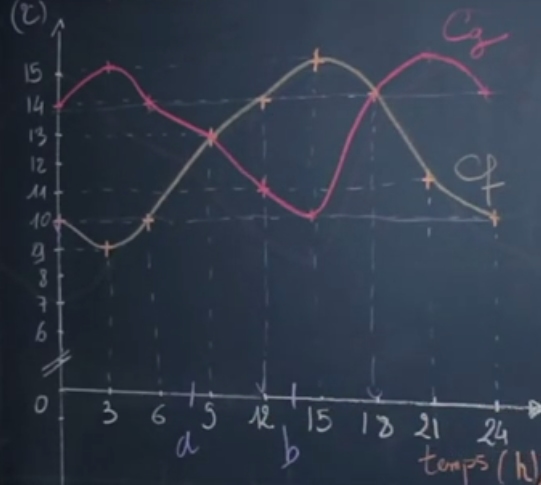
Soient $f$ et $g$ deux fonctions représentant l’évolution de la température au cours du temps.
Pour trouver le maximum de $f$, il faut regarder à quel instant la température est maximale. Il est atteint à $t = 15$.
Pour trouver le minimum de $f$, il faut regarder à quel instant la température est minimale. Il est atteint à $t = 3$.
Définition
Soit $f$ une fonction définie sur $D$, son ensemble de définition.
1) $M$ est un maximum de $f$ si pour tout $t \in D$, $f(t) \leq M$.
2) $m$ est un minimum de $f$ si pour tout $t \in D$, $f(t) \geq m$.
En d’autres termes, cette première inégalité signifie que la température est toujours plus petite que $M$ qui est le maximum.
On utilise la variable $t$ car on regarde l’évolution en fonction du temps, mais dans la plupart des cas, la variable utilisée sera $x$ sans que cela change la définition du maximum.
Le maximum de $f$ sur $[0; 24]$ est 15 et il est atteint en $t = 15$.
La température maximale est donc de 15°C et est atteinte à 15h.
Le minimum de $f$ sur $[0; 24]$ est 9 et il est atteint en $t = 3$.
Fonctions croissantes, décroissantes
Fonctions croissantes, décroissantes
Fonctions croissantes, décroissantes
Définitions.
Soit $f$ une fonction définie sur un intervalle $I$.
a) Pour tous réels $a$ et $b$ appartenant à $I$ tels que $a \leq b$,
si $f(a) \leq f(b)$ alors la fonction est croissante.
b) Pour tous réels $a$ et $b$ appartenant à $I$ tels que $a \leq b$,
si $f(a) \geq f(b)$ alors la fonction est décroissante.
Exemples
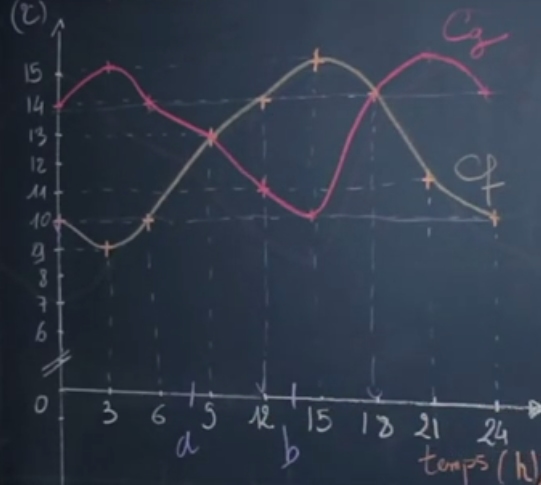
Soient deux fonctions $f$ et $g$ représentant l’évolution de la température en fonction du temps.
Considérons la fonction $f$ sur $[3; 15]$.
$f$ est croissante sur cet intervalle, la température augmente entre 3h et 15h.
Considérons de même la fonction $g$ sur $[3; 15]$.
$g$ est décroissante sur cet intervalle, la température diminue entre 3h et 15h.
Tableaux de variations
Tableaux de variations
Les tableaux de variation utilisent les notions de maximum, minimum et de fonctions croissante, décroissante et retranscrivent les variations de la fonction considérée.
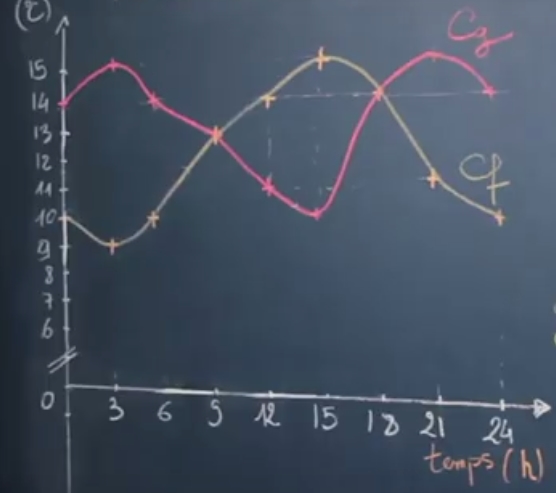
Un tableau de variation se présente toujours de la même façon. Voici un exemple pour les fonctions suivantes :
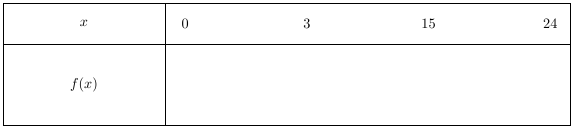
Etapes pour construire un tableau de variations
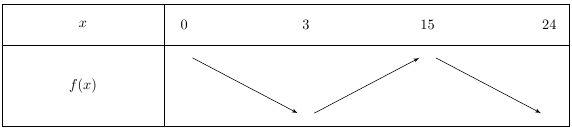
1) Sur la ligne du haut se trouvent les valeurs de la variable variant entre les bornes de l’ensemble de définition de la fonction.
Ici de $0$ à $24$.
Il faut ensuite regarder les valeurs de la variable pour lesquelles il y a un changement de variations, c’est à dire les points où la fonction admet un maximum ou minimum local.
Puis il faut placer ces valeurs dans la première ligne du tableau.
Ici, la fonction $f$ change de sens de variations (elle est d’abord décroissante puis croissante) en $t = 3$ et change à nouveau en $t = 15$.
2) Puis, pour symboliser que la fonction est décroissante sur l’intervalle $[0; 3]$ on trace une flèche vers le bas, puis une flèche vers le haut pour représenter la croissance de la fonction entre $[3; 15]$ puis à nouveau une flèche vers le bas entre $[15; 23]$.
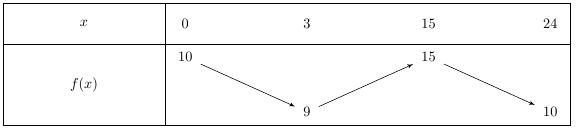
3) Enfin, aux extrémités des flèches, il faut écrire l’image par la fonction $f$ des nombres inscrits sur la première ligne.
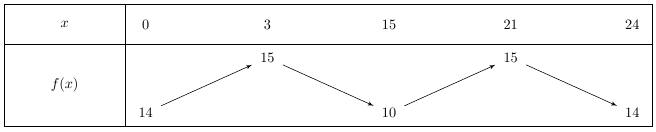
De même pour $g$, les points intermédiaires où la fonction change de sens de variation sont $3; 15; 21$.