Sens de variation d'une fonction
Sens de variation d'une fonction
Sens de variation d’une fonction
Définitions
Soit $f$ une fonction définie sur un intervalle $I$.
$\bullet$ $f$ est dite croissante sur $I$ si et seulement si, pour tous réels $a,b$ de $I$, $a\leqslant b \Rightarrow f(a)\leqslant f(b)$.
$\bullet$ $f$ est dite décroissante sur $I$ si et seulement si, pour tous réels $a,b$ de $I$, $a \leqslant b \Rightarrow f(a)\geqslant f(b)$.
$\bullet$ $f$ est monotone sur $I$ si $f$ est croissante sur $I$ ou bien si} $f$ est décroissante sur $I$.
$\bullet$ $f$ admet un maximum en $x_0\in I$ $\Leftrightarrow$ pour tout réel $x\in I$, $f(x)\leqslant f(x_0)$.
$\bullet$ $f$ admet un minimum en $x_0\in I$ $\Leftrightarrow$ pour tout réel $x\in I$, $f(x)\geqslant f(x_0)$.
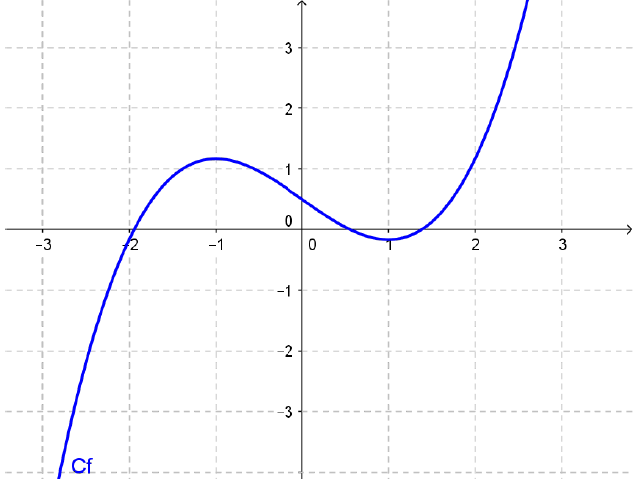
Illustration graphique
Ici, la fonction représentée est :
- croissante sur $I_1=[-2,-1]$
- décroissante sur $I_2=[-1,1]$
- croissante sur $I_3=[1,2]$
En revanche, on ne peut pas dire que $f$ est monotone sur $I=I_1\cup I_2 \cup I_3$ car $f$ change de sens de variation sur cet intervalle $I$.
Sens de variation d'une fonction - Exercice 1
1) Donner les variations de \(f\) et \(g\).
2) Étudier les positions relatives de \(C_f\) et \(C_g\).
- Étape 1 : On n’oublie pas de donner les ensembles de définition des fonctions.
- Étape 2 : On dresse le tableau de variation de chaque fonction.
- Étape 3 : On étudie graphiquement les positions relatives de \(C_f\) et \(C_g\).