Composition d’un système chimique : concentration en quantité de matière et en masse, détermination et absorption
Déterminer une quantité de matière
Ce cours du chapitre constitution et transformations de la matière se concentre d’abord sur la détermination d’une quantité de matière (espèces solides, liquides, en solution). Ensuite, il aborde l’absorption et la loi de Beer-Lambert. Enfin, il explique les concentrations molaire et massique.
Déterminer une quantité de matière : ce que tu vas réviser
Comment déterminer une quantité de matière ?
Déterminer une quantité de matière c’est déterminer le nombre de moles $n$ qui s’exprime en $mol.$ On a la masse molaire, le volume, la masse volumique, la concentration molaire et la concentration massive.
• $M$ la masse molaire (masse d’une mole d’espèce chimique) qui s’exprime en $g.mol^{-1}.$ Les masses molaires atomiques sont précisées dans le tableau périodique et on les donnera. La masse molaire d’un ion est environ égal à la masse molaire de l’atome correspondant. Quand on a la masse molaire d’une molécule à déterminer, il suffit de faire la somme des masses molaires atomiques qui constituent cette molécule. Dans le cas de la molécule d’eau, ce sera : $M(H_2O) = 2 \times M(H) + M(O)$.
Ensuite on utilise la masse $m$ qui s’exprime normalement en $kg$ mais en chimie on l’exprime couramment en $g.$
• $V$ le volume, qui normalement s’exprime en $m^3$ mais en chimie on l’exprime en $L.$
• $ρ$ la masse volumique qui s’exprime normalement en kg.m-3, mais on peut aussi la voir exprimée en $g.L^{-1}, kg.L^{-1}, g.mL^{-1}.$ Il faut savoir que les $kg.L^{-1}$ sont équivalents aux $g.mL^{-1}$ et quand on fait les conversions $L/m^3,$ il faut se souvenir de la relation qui permet de faire les conversions : $1 \ dm^3 = 1 \ L.$
• $C$ la concentration molaire qui s’exprime en $mol.L^{-1}.$
• $C_m$ (ou $t$ le titre massique) la concentration massique qui s’exprime en $kg.L^{-1}$ ou en $g.L^{-1}.$
Attention ! La concentration massique a la même unité que la masse volumique mais ce ne sont pas du tout les mêmes grandeurs. Pour la concentration massique, c’est la masse de soluté par litre de solution et pour la masse volumique, c’est la masse d’un litre d’espèce chimique mais c’est la même espèce chimique dans le cas de la masse volumique.
Voyons comment déterminer la quantité de matière dans le cas où l’on a une espèce solide, une espèce liquide ou une espèce en solution.
Espèces solides
Si on a une espèce solide, souvent, on nous donne la masse de solide. On va alors utiliser la formule : $n = \dfrac{m}{M}$.
C’est le cas le plus simple avec $n$ la quantité de matière en mol, $m$ la masse en $g$ et $M$ la masse molaire en $g.mol^{-1}.$ Les masses molaires sont très souvent données en $g.mol^{-1}$ donc si on a une masse en $kg$, il faut penser à la convertir en $g$ pour que les unités soient cohérentes. De manière générale, il faut toujours vérifier que les unités sont cohérentes.
Espèces liquides
Si on a une espèce liquide, on n’aura souvent pas la masse mais le volume. On reprend la formule : $n = \dfrac{m}{M}$.
Et puisqu’on n’a pas la masse mais le volume on va « convertir » la masse en volume en utilisant la masse volumique : $ ρ =\dfrac{m}{V}$.
On obtient alors la formule : $ n =\dfrac{ ρ\times V}{M}$.
Il faut alors faire attention car la masse volumique peut être exprimée dans différentes unités. Le nombre de moles $n$ s’exprime en mol, le volume $V$ en litres et la masse molaire $M $en $g.mol^{-1}.$ Il faut donc que la masse volumique soit en $g.L^{-1}$ pour que les unités soient cohérentes. Il faut bien penser à faire les conversions nécessaires.
Espèces en solution
Si on a une espèce en solution, on utilise la relation : $n = C\times V_{sol}$.
Le nombre de moles $n$ s’exprime toujours en mol, la concentration molaire est exprimée en $mol.L^{-1}$ et le volume de la solution doit être exprimé en $L,$ pour que les unités soient cohérentes. Parfois, on donne la concentration massique et non pas la concentration molaire. On peut trouver une relation entre la concentration massique et la concentration molaire.
Donc : $C_m = \dfrac{m}{V_{sol}}$.
Or la masse est aussi égale au nombre de moles multiplié par la masse molaire : $C_m = \dfrac{n\times M}{V_{sol}}$.
On reconnaît : $\dfrac{n}{V}$, l’expression de la concentration molaire.
On a alors : $n = C\times M$.
Le nombre de moles vaut : $n = n = \dfrac{C_m}{M} \times V_{sol}$.
Il n’est pas nécessaire d’apprendre cette formule par cœur, on peut la retrouver avec le raisonnement précédent. $n$ est le nombre de moles en $mol,$ $C_m$ est la concentration massique en $g.L^{-1},$ $M$ la masse molaire en $g.mol^{-1}$ et $V_{sol}$ le volume de la solution en $L.$
Si on a des doutes sur une formule, on peut vérifier qu’elle est cohérente en faisant une analyse dimensionnelle (en analysant les unités). Si la concentration massique est exprimée en $g.L^{-1},$ le volume de la solution est exprimé en $L,$ et la masse molaire s’exprime en $g.mol^{-1}.$ Les grammes se simplifient, $L$ et $L^{-1}$ se simplifient aussi, on obtient alors l’inverse des $mol^{-1}$ qui vaut des mol. C’est bien l’unité de $n.$ À priori, on sait que notre formule est cohérente.
Pour aller plus loin dans « Constitution et transformations de la matière »
Après avoir étudié ce cours, nous te conseillons de poursuivre avec ces autres notions :
Absorption et loi de Beer-Lambert
Déterminer la concentration avec la loi de Beer-Lambert : ce que tu vas réviser
I. Solutions colorées et absorbance
Comment lire un spectre d’absorption ?
Une solution est colorée si elle absorbe des radiations de la lumière visible. Si on envoie une lumière incidente, par exemple une lumière blanche, sur une solution colorée, une partie de la lumière est absorbée et une autre partie est transmise. Une solution est transparente et incolore si elle n’absorbe pas de lumière dans le spectre de la lumière blanche.
Comment réaliser un spectre d’absorption ?
On détermine l’absorbance qui est une grandeur qui compare la lumière transmise à la lumière incidente. L’absorbance est notée $A$ et elle est sans unités. Pour une solution colorée, on peut tracer le spectre d’absorption de cette solution colorée. Par exemple ci-dessous, le spectre d’absorption du permanganate de potassium.
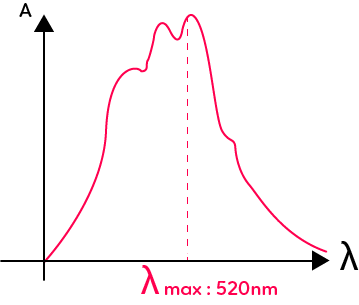
Pour tracer ce spectre d’absorption, on utilise un spectrophotomètre et on mesure pour chaque longueur d’onde du spectre de la lumière blanche, l’absorbance de la solution. On peut déterminer la valeur maximale de l’absorption : $λ_{max}.$ Pour le permanganate de potassium, on a une valeur de $520$ nm située dans le domaine du vert. Cela est normal puisque la solution de permanganate apparaît magenta et absorbe au maximum dans sa couleur complémentaire qui est le vert.
II. Déterminer la concentration
À partir de l’absorbance, on peut déterminer la concentration en espèce colorée d’une solution. Pour rappel, la concentration est une grandeur qui est égale au nombre de moles par le volume de solution (mol/L) et qui peut être égale à la masse de soluté par le volume de solution (en g/L) pour la concentration massique. Il y a plusieurs possibilités pour déterminer la concentration d’une solution colorée.
L’échelle de teintes
En effet, plus la solution est concentrée en espèce colorée et plus elle est foncée. On le voit ici avec C1, C2, C3, C4. La concentration augmente de droite à gauche.
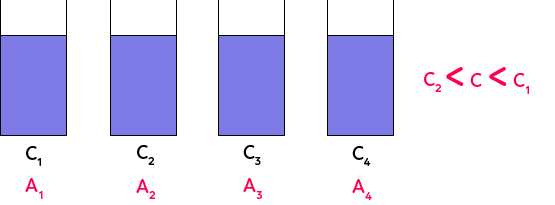
Si on a une solution de permanganate dont on ne connaît pas la concentration, on peut essayer de la placer dans l’échelle de teintes en comparant la teinte de la solution de concentration inconnue et la teinte des solutions de concentrations connues ici. Si par exemple, on arrive à placer la solution de concentration inconnue entre la solution 1 et la solution 2, on peut dire que : C2 < C < C1. On n’aura pas la valeur exacte de la concentration, mais juste un encadrement. Pour avoir la valeur exacte, on utilise la loi de Beer-Lambert et l’absorbance.
Loi de Beer-Lambert
Pour chaque concentration, on mesure l’absorbance A1, A2, A3, A4. On mesure l’absorbance en fixant la longueur d’onde pour se placer à la longueur d’onde du maximum d’absorption. Plus la concentration diminue et plus le spectre s’étale. Donc, si on ne se met pas à la longueur d’onde du maximum d’absorption, au bout d’une certaine concentration on aura des valeurs qui seront trop faibles à exploiter. Ensuite, on trace la courbe qui représente l’absorbance en fonction de la concentration et on obtient une droite qui passe par l’origine. C’est la loi de Beer-Lambert.
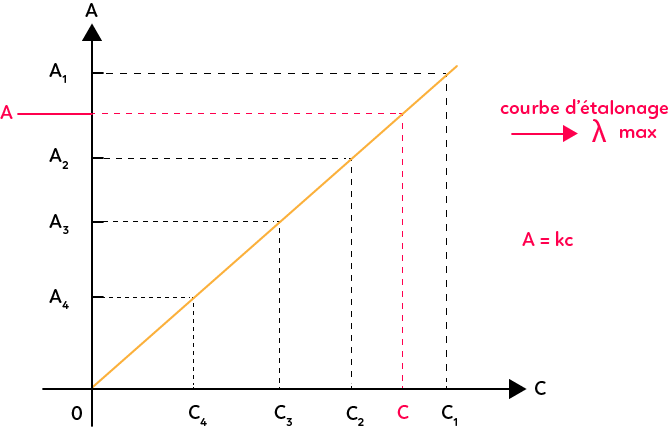
Puisqu’on a une droite qui passe par l’origine cela veut dire que l’absorbance est proportionnelle à la concentration : $A = k.C.$
Comment trouver $k$ dans la loi de Beer-Lambert ?
$k$ est la constante de proportionnalité qui dépend de la longueur d’onde à laquelle on fait l’étude, ici $λ_{max},$ et qui dépend aussi d’autres paramètres : substance colorée, épaisseur de la cuve, etc. Voilà pourquoi il faut toujours utiliser une même cuve. Cette courbe s’appelle la courbe d’étalonnage et on peut l’utiliser pour déterminer la concentration de la solution de concentration inconnue. Pour déterminer cela, on mesure son absorbance, que l’on note $A,$ dans les mêmes conditions que les autres solutions et on reporte $A$ en ordonnées sur la courbe. On lit en abscisses la concentration correspondante. Ainsi, on a une méthode précise pour déterminer la concentration de solutions colorées.
Pour aller plus loin dans « Constitution et transformations de la matière »
Après avoir étudié ce cours, nous te conseillons de poursuivre avec ces autres notions :
Concentration en quantité de matière et concentration en masse
Concentration molaire et concentration massique : ce que tu vas réviser
I. Définition de la concentration molaire et massique
La concentration en quantité de matière correspond à la concentration molaire.
La concentration en masse correspond à la concentration massique.
A. Position du problème
On peut s’intéresser à deux situations :
a) n = 2 mol de NaCl dans 3 L d’eau.
b) m = 40 g de NaCl dans 3 L d’eau.
Quelles grandeurs pour quantifier la quantité de NaCl dans 1 L d’eau salée ?
B. Comment calculer la concentration en quantité de matière ?
On a cette formule : $C = \dfrac{n}{V}$. $C$ est la concentration en quantité de matière en mol.L-1 et vaut la quantité de matière en mol divisée par le volume en L.
On peut s’intéresser à l’application de cette formule dans le premier cas, le cas a). Dans ce cas, on a : $c = \dfrac{n}{V}= \dfrac{2}{3} = 0,67 \ mol.L^{-1}$.
Si on a ajouté 2 mol de sodium dans 1 L d’eau, on a une concentration en quantité de matière dans notre solution de 0,67 mol.L-1 de chlorure de sodium.
C. Comment calculer la concentration en masse ?
La concentration en masse correspond à cette formule : $C_m = \dfrac{m}{V}$. Donc la concentration en masse $C_m$ en g.L-1 est égale à la masse en g divisée par le volume en L.
Dans le cas b), on a : $C_m = \dfrac{m}{V} = \dfrac{40}{3} = 13,3 \ g.L^{-1}$.
II. Relations entre les formules
A. Formules de la concentration molaire, du volume et de la masse
La formule à connaître est cette formule : $C = \dfrac{n}{V}$.
On peut obtenir cette formule : $n = C\times V$ en multipliant les termes de gauche et de droite par $V.$
De même pour la formule avec le volume : $V = \dfrac{n}{C}$, qui peut se retrouver facilement grâce à la première formule.
De la même manière pour la concentration en masse, on doit connaître cette formule : $C_m = \dfrac{m}{V}$, mais pas $m = C_m \times V$ et $V = \dfrac{m}{C_m}$, qui se retrouvent facilement grâce à la première formule.
B. Relation entre la concentration en quantité de matière et la concentration en masse
On connaît la relation avec la masse molaire : $M = \dfrac{m}{n}$.
$M,$ la masse molaire, s’exprime en g.mol-1. On peut aussi écrire que $m =M\times n$.
On a la formule de la concentration en masse : $C_m = \dfrac{m}{V} = \dfrac{M\times n}{V} = M\times C$.
Pour aller plus loin dans « Constitution et transformations de la matière »
Après avoir étudié ce cours, nous te conseillons de poursuivre avec ces autres notions :


