FONCTIONS DU SECOND DEGRÉ

Fonction du second degré - Le rappel de cours

1) Définition 

Pour tout $x \in \mathbb{R}$, une fonction $f$ du second degré peut se mettre sous la forme canonique :

$f(x) = a(x - \alpha)^2 + \beta$, où $a \neq 0$. 

2) Variations 

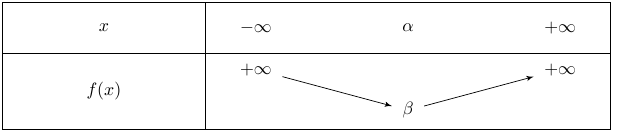
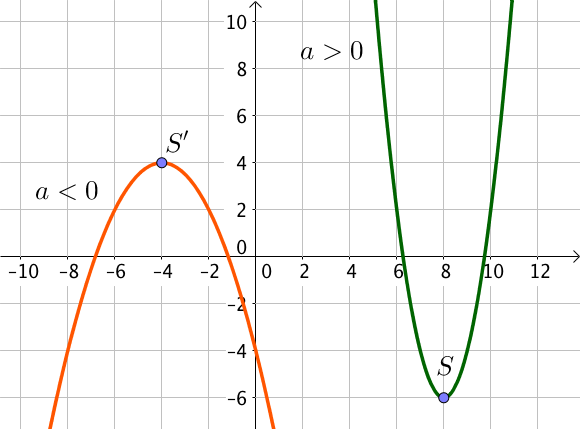
Si $a>0$, la représentation graphique de la fonction est une parabole tournée vers le haut qui admet un minimum atteint en $x= \alpha$ valant $\beta$.

Son tableau de variation est le suivant :

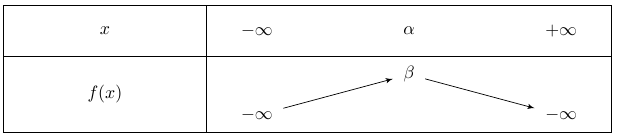
Si $a<0$, la représentation graphique de la fonction est une parabole tournée vers le bas qui admet un maximum atteint en $x= \alpha$ valant $\beta$.

Son tableau de variation est le suivant :

Dans les deux cas, le sommet de la parabole est $S(\alpha; \beta)$. 

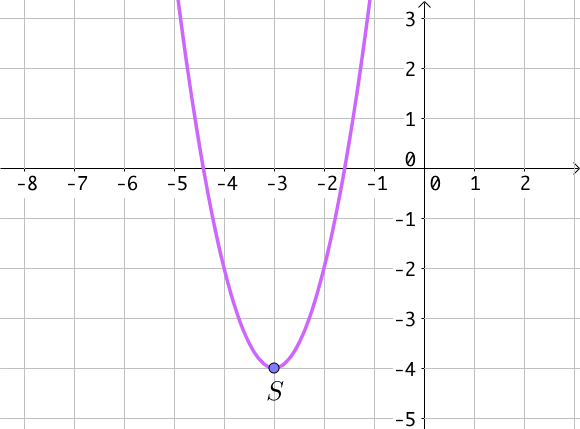
3) Exemple

Soit $f(x) = 2(x + 3)^2 - 4$,

Cette fonction est décroissante puis croissante. Elle admet un minimum ayant pour coordonnées $S(-3; -4)$.