Dénombrement : principes additif et multiplicatif
Dénombrement : principes additif et multiplicatif
En mathématique, dénombrer c’est compter le nombre d’objets d’un ensemble.
-
Le principe additif
Lorsque l’on doit dénombrer un ensemble, on va procéder à une classification sur les objets de l’ensemble, et pour connaitre le nombre total d’objets, nous allons compter le nombre d’objets par classe de la classification.
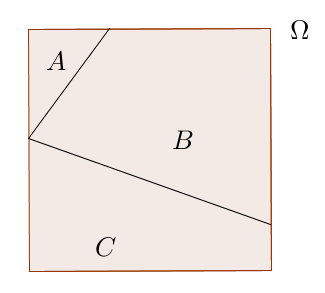
Si on a une ensemble $\Omega$, on cherche à dénombrer le nombre d’éléments de $\Omega$. On établit ainsi une classification. Ici il y a 3 classes : A, B, et C. Dans A il y a 4 éléments, dans B il y a 3 éléments et dans C il y en a 5. On note le nombre d’éléments de $\Omega$ (le cardinal de $\Omega$ ) de cette manière : $|\Omega |$
$|\Omega |=|A|+|B|+|C|$
Cette propriété est vraie à certaines conditions :
Il faut que tous les éléments soient comptés au moins une fois :
$A\cup B\cup C=\Omega$
On n’oublie aucun élément de $\Omega$
Il ne faut pas compter plusieurs fois le même élément :
$A\cap B=A\cap C=B\cap C=\varnothing$
La classification doit être non redondante : chaque élément doit être compté au plus une fois., ce qui signifie qu’il n’y a pas d’élément qui soit présent dans deux classes différentes.
Prenons un exemple de classification :
Dans une classe il y a 14 filles et 20 garçons. Donc au total 20+14=34 élèves.
Prenons maintenant un exemple ou il faut faire attention :
Dans un classe de 34 élèves, tous étudient au moins une LV anglais ou allemand : 23 étudient l’anglais, 20 étudient l’allemand. Combien étudient les 2 LV ?
La classe correspond à $\Omega$. Les élèves qui étudient l’allemand correspondent à l’ensemble A et ceux qui étudient l’anglais correspondent à l’ensemble B.
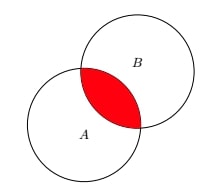
Il y a des élèves qui étudient les deux langues.
Ainsi, si on dit que $|\Omega |=|A|+|B|$, on compte deux fois les élèves qui étudient les deux langues : on les compte en tant que germanistes et en tant qu’anglicistes. S’ils sont comptés deux fois, il faut enlever une fois les éléments qui se situent à l’intersection de A et B.
On obtient donc la formule suivante (très similaire à celle des probabilités) :
$|\Omega |=|A|+|B|-|A\cap B|$
Donc $|A\cap B|=|A|+|B|-|\Omega |=43-34=9$
Il y a donc 9 élèves qui étudient les deux langues.
Dans cette exemple, la condition d’unicité donnée plus haut n’est pas vérifiée car certains éléments sont dans les deux classes à la fois. On ne peut donc pas dire $|\Omega |=|A|+|B|$
-
Le principe multiplicatif
Prenons un exemple :
Un restaurant propose à sa carte 2 entrées, 4 plats principaux (PP) et 3 desserts. On constitue un menu avec une entrée, un PP et un dessert. Le but est de dénombrer le nombre de menus possibles.
Lors du premier choix on a deux branches car 2 entrées possibles, lors du deuxième on a 4 branches pour chaque premier choix (car 4 plats principaux possibles). Et enfin, pour chaque extrémité il y a 3 choix possibles pour les 3 desserts au choix.
Chaque branche correspond à un menu différent, il suffit maintenant de compter le nombre de branches, c’est-à-dire le nombre d’extrémités sur la dernière colonne.
On a donc $2\times 4\times 3=24$ menus possible avec 2 qui correspond au nombre de choix d’entrée, 4 au nombre de choix de PP et 3 au nombre de choix de dessert.
Écrivons le de manière plus théorique :
On considère les 3 ensembles suivants :
- E : L’ensemble des entrées
- P : L’ensemble des PP
- D : l’ensemble des desserts
Un menu correspond donc à un triplet $(e, p, d)\in E\times P\times D$, avec e dans E, p dans P et d dans D.
$E\times P\times D$ correspond au produit cartésien des ensembles.
On a donc : $ E\times P\times D=|E|\times |P|\times |D|$
Une autre façon de voir la chose: le syndrome de l’autoroute
Lorsque sur l’autoroute il y a 3 sorties principales et sur chaque sortie principale il y a 2 sortie secondaire, il n’y a pas 3+2 sorties totales mais 3×2 sorties totales.
-
Ensemble de k-uplets dans une ensemble E à n éléments
Prenons maintenant un cas particulier :
On prend tous les éléments du triplet dans le même ensemble. On cherche l’ensemble de
k-uplets dans une ensemble E à n éléments : [|1,n|]=E
On doit donc déterminer un k-uplet : (x,x,…,x,x)
Pour chaque x, il y a n choix possibles. D’après le principe multiplicatif, il y a $n^k$
Donc dans un produit cartésien, lorsque les ensembles sont répétés ($E\times E\times…\times E$) on peut écrire :
$|E^k|=|E|^k$
On est dans un modèle de tirage avec ordre (l’ordre importe) et avec répétition (on peut avoir plusieurs fois le même élément dans le k-uplet)
Prenons un exemple :
Un sac contient 8 jetons numérotés de 1 à 8.
On tire successivement (donc l’ordre compte) et avec remise (il peut donc y avoir des répétitions) 3 jetons.
Le but est de déterminer le nombre de résultats possibles : le nombre de triplet de la forme $(J_1,J_2,J_3)$ avec $J_1$ le numéro du premier jeton tiré, $J_2$ le numéro du deuxième jeton tiré, $J_3$ le numéro du troisième jeton tiré.
Comme il y a un ordre et répétition, il y a 8 choix pour le premier, 8 pour le deuxième et 8 pour le troisième : il y a $8^3=512$ choix possibles.
Il est donc nécessaire de se poser la question de l’ordre et de la répétition dans ce type d’exercice.